Как определить полярность автомобильного аккумулятора?
Многие автомобилисты знают, что может произойти в случае путаницы с аккумуляторными клеммами. Да, это случается не специально, а по причине недостаточного опыта. В автомобилях отечественного производства и многих иномарках полярность аккумулятора различается. Автомобилисты-аматоры, зачастую не знают о таком термине и о существовании каких-либо различий между видами полярности. Данная статья поможет разобраться в указанной теме и ответит на вопросы касательно полярности аккумуляторов.
Что такое полярность аккумулятора?
Понятие полярности подразумевает под собой расположение внешних клемм аккумулятора, которые ещё называют токовыводами, на крышке АКБ или её лицевой стороне. Принято выделять две самые распространённые схемы полярности – прямую и обратную. Проще говоря, в одной схеме минусовая клемма находится слева, в другой — справа.
Важно!
Какие полярности АКБ бывают?
У вас приблизительно уже должно складываться понятие полярности и её видов. Но как определить, заглянув под капот, какая полярность у вашей АКБ, прямая или обратная? Аккумуляторные батареи с прямой полярностью устанавливаются на большинство отечественных автомобилей. Но что такое прямая полярность аккумулятора и каким образом она определяется? На самом деле всё предельно просто. Возьмите АКБ, разверните её к себе лицевой стороной. У вас перед глазами должна оказаться этикетка, а клеммы снизу. 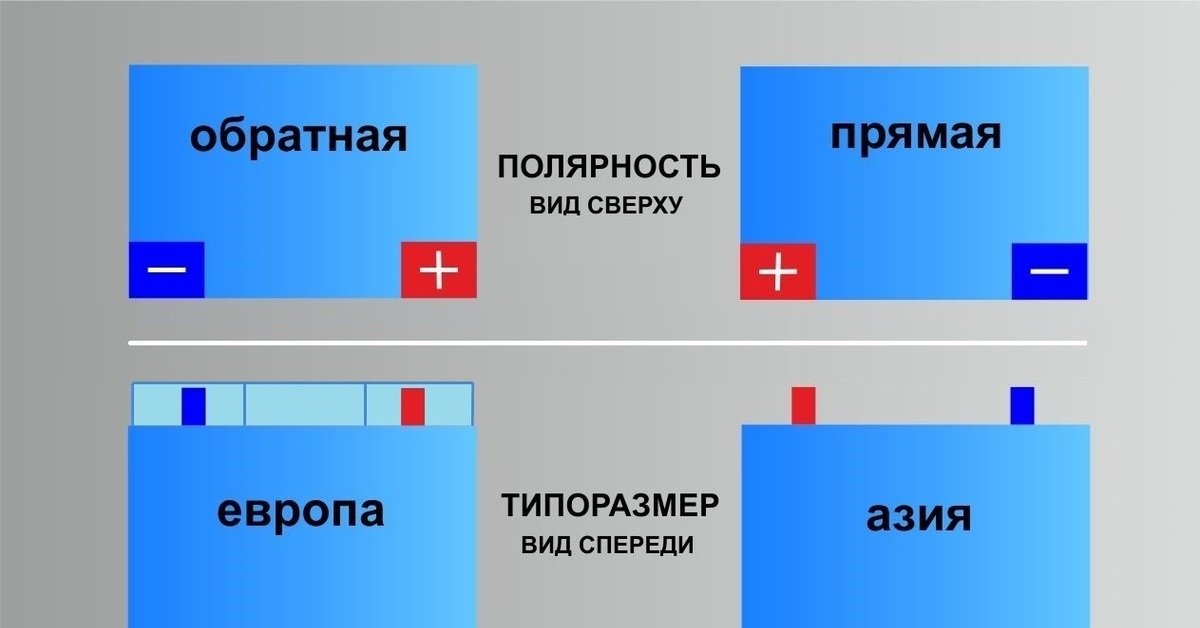 АКБ такого типа стоят на большинстве автомобилей отечественного производства.
АКБ такого типа стоят на большинстве автомобилей отечественного производства.
Обратная полярность – это разработка европейских инженеров. На 90% европейских автомобилей ставится аккумулятор с обратной полярностью. Она отличается от прямой только развёрнутым расположением клемм. Для её определения проделайте те же манипуляции, что и с прямой. Только теперь минусовой токовывод будет находится слева, а плюсовой – справа.
Интересный факт! Европейские аккумуляторы отличаются от азиатских не только габаритами, формой, расположением клемм, а ещё и их диаметром. Стандарты Европы: плюсовая клемма — 19,5 мм, минусовая — 17,9 мм. В Азии они меньше: плюс — 12,7 мм, минус — 11,1 мм.
Как ещё можно определить прямую и обратную полярность АКБ автомобиля? Если не брать в расчёт полюса, то «на глаз» их различить практически невозможно.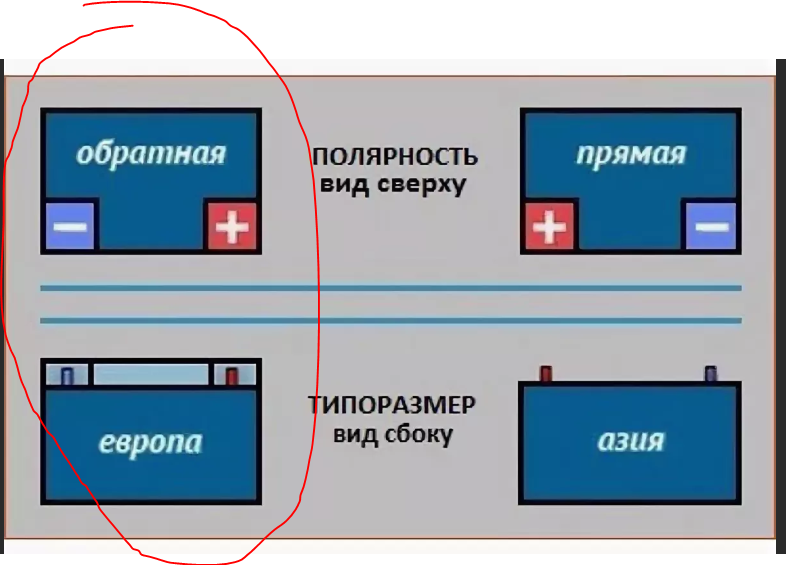
Как узнать, полярность 0 — это прямая или обратная? Запутать себя разнополярными аккумуляторами очень просто, так как можно приобрести АКБ с неподходящим расположением токовыводов. Прямая полярность – это единица, обратная – это ноль. Конечно для таких случаев можно купить переходник с прямой полярности на обратную, но это тоже не выход, поскольку это не совсем удобно. Даже опытные водители, совершив спонтанный выбор, попадаются в сети случая.
Важно! Если ваших знаний недостаточно, обратитесь к консультанту магазина автозапчастей и попросите подобрать аккумулятор для вашего автомобиля. У продавцов должны быть каталоги АКБ с деталным описанием каждой. Это наиболее оптимальный вариант.
Можно ли установить аккумулятор другой полярности?
Это достаточно частый вопрос водителей, имеющих недостаточный опыт.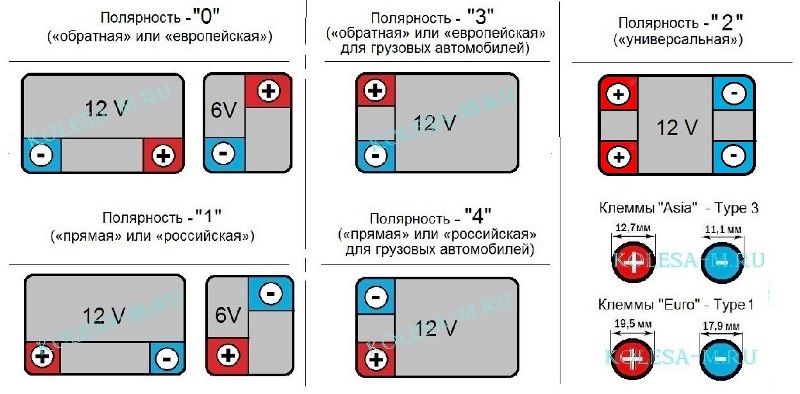 Порой новички не только покупают первый понравившийся аккумулятор, но ещё и сразу устанавливают его на автомобиль. Везёт тем, кто «попал пальцем в небо», но в других случаях придётся худо.
Порой новички не только покупают первый понравившийся аккумулятор, но ещё и сразу устанавливают его на автомобиль. Везёт тем, кто «попал пальцем в небо», но в других случаях придётся худо.
Если в свой автомобиль подключить аккумулятор не той полярности, может сгореть вся электроника вместе с мозговым центром
Но может случиться и так, что об ошибке вы узнали только после установки, когда клеммы ободрались и замкнули, а в магазине вам отказались менять батарею, аргументируя это тем, что это не гарантийный случай. Как поступать?Постарайтесь продать такую АКБ. Поясните причину продажи и далее будьте внимательнее. Если никто не покупает, что уже поделать, всё равно придётся брать новый «правильный» аккумулятор.
Интересный факт! Все аккумуляторные батареи до середины прошлого века имели напряжение только в пределах 6 Вольт.
Подписывайтесь на наши ленты в таких социальных сетях как, Facebook, Вконтакте, Instagram, Pinterest, Yandex Zen, Twitter и Telegram: все самые интересные автомобильные события собранные в одном месте.
Полярность 0 это прямая или обратная
Определение полярности АКБ
У автомобильных аккумуляторов бывает полярность двух видов: прямая и обратная. Иногда продавцы аккумуляторов говорят «аккумулятор с правым плюсом» или «аккумулятор с левым плюсом». Во всех этих случаях речь идет о расположении положительной и отрицательной клемм аккумулятора (полюсных выводов).
Для правильно определения полярности аккумулятора в легковом автомобиле, его необходимо развернуть к себе, как на рисунке:
Непосредственно на выводах, либо рядом с ними обязательно должны быть значки «+» и «-», которые обозначают полюса.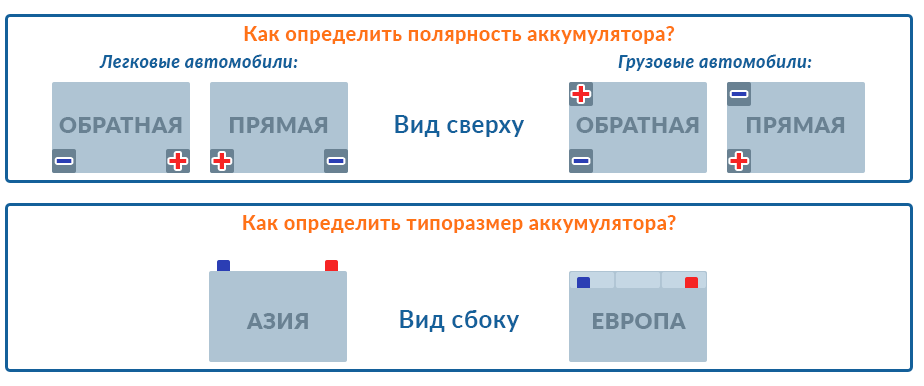
- Если плюс справа, то это аккумулятор обратной полярности. Ее могут называть также «евро полярность» или обозначать «0» или «R».
- Если плюс слева, то это прямая полярность. Ее могут называть также «стандартная, «1» или «L».
Как правило, на отечественных легковых автомобилях установлены аккумуляторы, имеющие прямую полярность. На иномарках же в ходу обратная полярность.
Совсем иначе обстоит дело с полярностью у аккумуляторов для грузовиков, автобусов, строительной и специальной техники емкостью более 110 Ач:
- «3» — «+» слева (евро, обратная). Для европейских грузовиков.
- «4» — «+» справа (стандартная, прямая). Для российских грузовиков.
Еще одна особенность АКБ — исполнение корпуса. Различают два основных:
— для азиатских автомобилей (китайских, корейских, японских, некоторых американских). У них клеммы выступают над крышкой корпуса. Они выше, чем европейские АКБ.
Они выше, чем европейские АКБ.
— для европейских авто. Клеммы утоплены в крышку аккумулятора. Они ниже азиатских АКБ.
Несколько слов об уходе за клеммами АКБ.
Уход за полюсными выводами аккумуляторной батареи сводится к выявлению и уничтожению следов коррозии. Следы коррозии выглядят как порошкообразные отложения белого или желтоватого цвета.
Для обработки клемм нужно:
- Снять аккумулятор с автомобиля.
- Обработать выводы батареи раствором воды с содой.
- Начнется реакция с образованием пузырьков. Выводы станут коричневого цвета.
- При необходимости зачистить выводы металлической щеткой.
- После завершения реакции вытереть полюсные выводы и саму батарею смоченной в холодной воде тряпкой и просушить аккумулятор.
- Поставить АКБ в гнездо на автомобиль.
- Нанести тонкий слой вазелина на клеммы и выводы. Это предотвратит дальнейшее образование коррозии.
- При выключенном зажигании подсоединить провода к полюсным выводам аккумулятора.

Полярность аккумулятора – обратная или прямая. Как определить полярность?
Аккумулятор (АКБ) – основной источник электрического тока в автомобиле, основными характеристиками которого являются номинальная емкость и ток холодного запуска, подаваемый на стартер. Однако есть еще одна характеристика, которая очень важна при выборе модели аккумуляторной батареи — его полярность, т.е. расположение внешних токовыводов (токовыводящих элементов «+» и «-») на лицевых панелях аккумулятора.Дело в том, что современный модельный ряд аккумуляторов представлен моделями отечественного и европейского производства и двумя основными вариантами полярности – прямой и обратной (прочие варианты встречаются крайне редко и в РФ не используются). В чем различие между ними, и почему важно выбирать АКБ с правильной полярностью, соответствующей техническим требованиям автомобиля?
Следует понимать, что разная полярность аккумуляторов никак не отражается на их производительности – батареи с прямой и обратной полярностью работают совершенно идентично. Разница только в геометрии токовыводов (лево-право) и ограничениях по применению — аккумуляторы с прямой полярностью используются в автомобилях отечественного производства, а обратная полярность характерна для батарей европейских и американских авто. Эти различия следует обязательно учитывать при подключении АКБ к клеммам стартера на автомобиле.
Разница только в геометрии токовыводов (лево-право) и ограничениях по применению — аккумуляторы с прямой полярностью используются в автомобилях отечественного производства, а обратная полярность характерна для батарей европейских и американских авто. Эти различия следует обязательно учитывать при подключении АКБ к клеммам стартера на автомобиле.
Прямая полярность
Российская (прямая) полярность аккумулятора маркируется цифрой «1» и подходит для большинства автомобилей отечественного автопрома (кроме некоторых моделей последнего поколения и экспортных комплектаций). В таких аккумуляторах на лицевой панели плюсовая клемма находится слева, а минусовая — справа. Чтобы исключить ошибки при подключении, на корпусе аккумулятора обычно токовыводы помечены значками «+» и «-».
Обратная полярность
Европейская (обратная) полярность – это практически полный модельный ряд европейских, японских, корейских и американских автомобилей.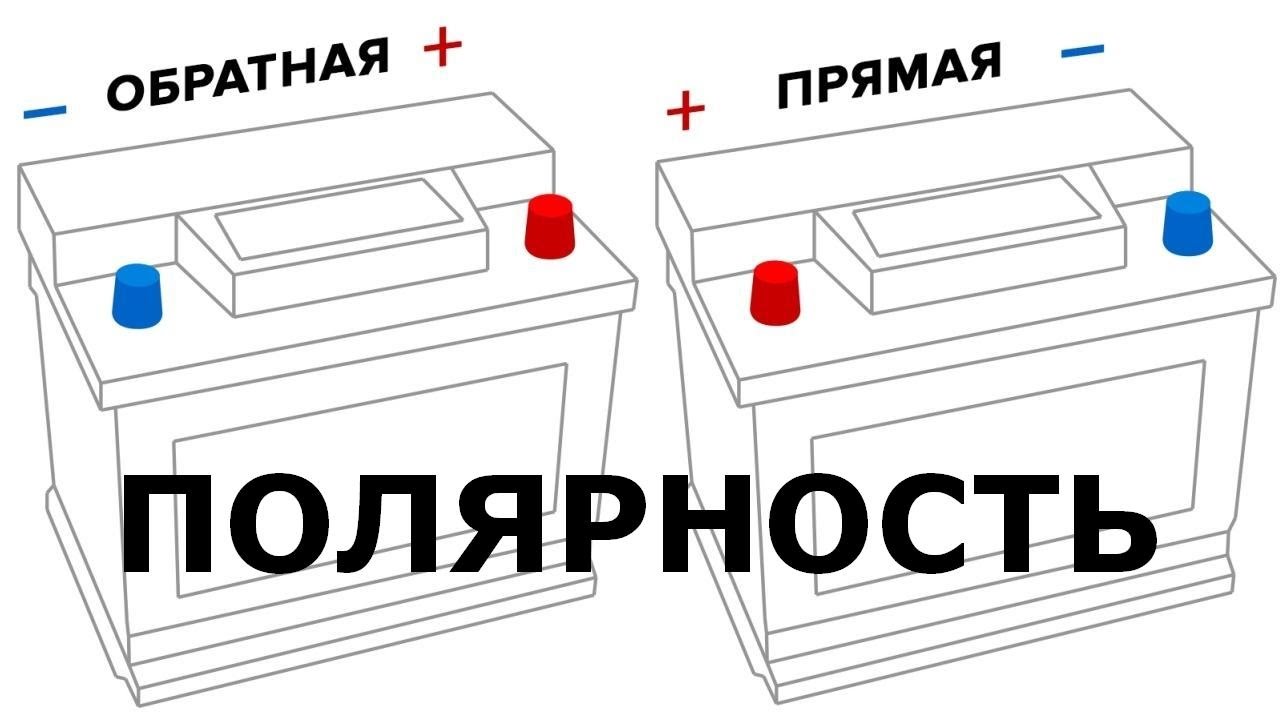 АКБ с обратной полярностью маркируются значком «0». В них плюсовая клемма будет на лицевой панели справа, а минусовая – слева.
АКБ с обратной полярностью маркируются значком «0». В них плюсовая клемма будет на лицевой панели справа, а минусовая – слева.
Существуют еще аккумуляторы с диагональным расположением токовыводов (маркируются значком «2»), а также европейские АКБ для грузовиков с обратной боковой полярностью («3»), и отечественные АКБ для грузовиков («4») с прямой боковой полярностью. Чтобы не ошибиться при их подключении, следует внимательно следить за цифровой маркировкой моделей батарей.
Почему это важно?
Купить по ошибке аккумулятор с неподходящей для автомобиля полярностью или неправильно подключить к АКБ клеммы может иногда даже опытный водитель: внешне и по техническим характеристикам батареи с прямой и обратной полярностью могут ничем не отличаться.
В тоже время, неправильное подключение полярностей опасно для автомобиля множеством неприятных последствий: быстрой разрядкой аккумулятора, коротким замыканием (горят предохранители), воспламенением электропроводки, разрушением самого аккумулятора, выходом из строя ЭБУ (бортового компьютера) или генератора, перегоранием предохранителей АКБ, системы освещения авто, сигнализации и печки.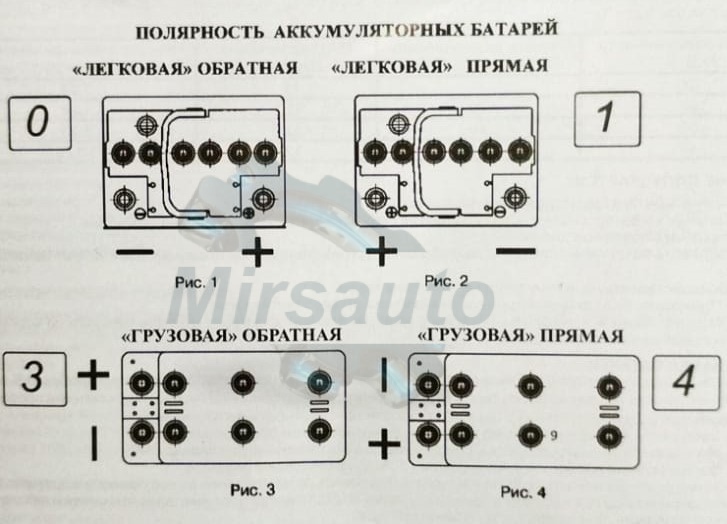 При неправильном подключении аккумулятора к зарядному устройству, сгорит зарядное устройство, а при подзарядке одного АКБ от другого («прикуривание») – могут сгореть обе батареи и даже оба автомобиля.
При неправильном подключении аккумулятора к зарядному устройству, сгорит зарядное устройство, а при подзарядке одного АКБ от другого («прикуривание») – могут сгореть обе батареи и даже оба автомобиля.
Самостоятельное определение полярности
Если номерная маркировка аккумуляторов и символы токовыводов («+» и «-») отсутствуют на корпусе батареи, воспользуйтесь тестером (мультиметр или вольтметр), который точно определит полярность токовыводов аккумулятора. Прибор, подключенный к токовыводам щупами, покажет наличие положительного напряжения при правильном подключении, и отрицательное — при неправильном.
Кроме того, на большинстве моделей АКБ положительный контакт чаще всего помечен красным цветом (обычно такая маркировка практически не стирается), а его размер обычно больше, чем у отрицательного токовывода. Следует помнить, что для некоторых моделей аккумуляторов американского производства эти методы определения полярности не действуют: сама батарея просто не имеет штырей токовыводов (вместо них выемки под контакты).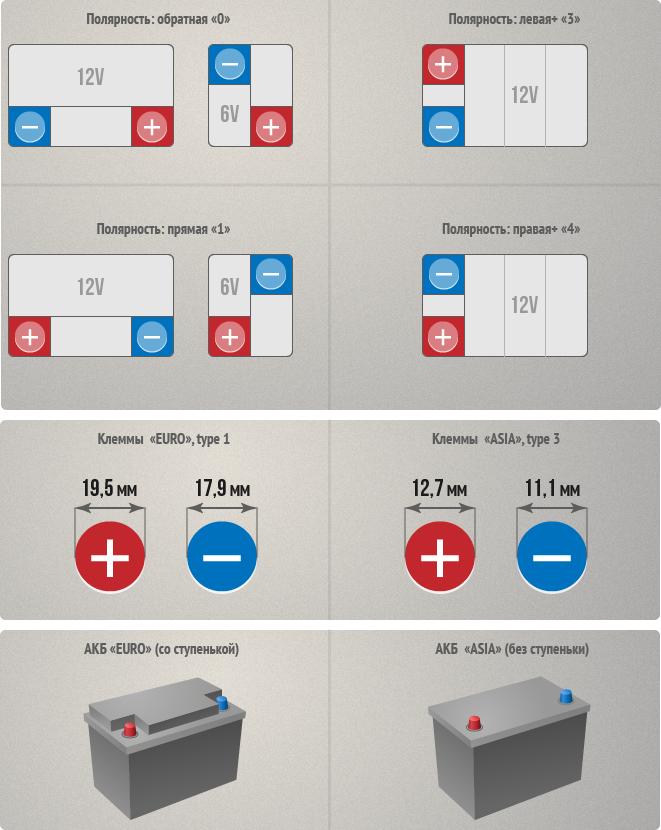
Использование аккумуляторов с неподходящей полярностью
Если вы по ошибке купили аккумулятор с полярностью, которая не соответствует техническим требованиям вашего автомобиля, то теоретически такой АКБ можно использовать (хотя и нежелательно), развернув его другой стороной в гнезде под капотом. Но вы рискуете столкнуться с тем, что вам не хватает длины одного из клеммных кабелей, который придется наращивать пусковыми проводами.
Специалисты не рекомендуют делать этого, так как можно ошибиться в расчете сечения кабеля и сжечь всю электрику на автомобиле. Проще поменять АКБ у продавца, а еще лучше – заранее разобраться с полярностью авто и при покупке сразу заказывать ту батарею, которая рекомендована производителем авто.
Как определить полярность аккумулятора?
Для правильного подбора аккумулятора важно правильно определить его полярность. Сделать это несложно. Для легковых аккумуляторов (емкостью от 35Ah до 110Ah), у которых клеммы (токовыводы) расположены вдоль длинной стороны, полярность определяется так:
разверните батарею к себе той стороной, вдоль которой расположены клеммы и на которой обычно размещается лицевая этикетка:
— если положительная клемма (токовывод) аккумулятора (рядом с ней на крышке аккумулятора должен быть нарисован «+») находится справа, то у аккумулятора полярность «0» («обратная» или «европейская»);
— если плюсовая клемма находится слева – у аккумулятора полярность «1» («прямая» или «российская»).
Для определения полярности грузовых аккумуляторов, если клеммы (токовыводы) расположены вдоль короткой стороны, нужно развернуть батарею этой стороной от себя. Тогда, если «+» справа — полярность «3» («обратная» или «европейская» для грузовых автомобилей), а если слева – у аккумулятора полярность «4» («прямая» или «российская» для грузовых автомобилей). Кроме того, могут встречаться грузовые аккумуляторы с полярностью «2» — клеммы у таких аккумуляторов расположены по диагонали, также существует полярность «9» (она же иногда обозначается цифрой «5») — в этом случае клеммы расположены посередине крышки аккумулятора.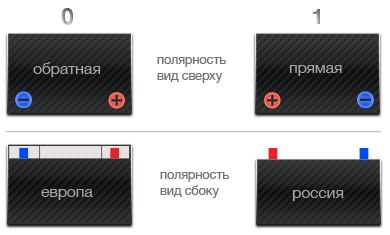
что это такое и как определить
Многие автолюбители, приобретая новую аккумуляторную батарею, обращают внимание только на ее рабочие параметры – напряжение, емкость, и размеры, забывая при этом о полярности. Сразу отметим, что этот термин у АКБ не относится к физике, а является исключительно конструктивным понятием. В результате, игнорирование полярности приводит к тому, что батарею просто не удается подключить к сети потому, что провода с клеммами не достают к выводам аккумулятора.
Что значит прямая или обратная полярность аккумулятора
Понятие «полярность» определяет положение клеммных выводов аккумуляторной батареи. Самыми распространенными являются два ее вида – прямая и обратная. Далее разберемся, что такое прямая и обратная полярность аккумулятора, как ее определить, и также некоторые полезные советы.
- Аккумуляторы с прямой полярностью – еще разработка советских инженеров, отсюда и второе ее название. Применяется она на батареях, производимых на постсоветском пространстве.
 Ее особенность заключается в том, что «плюсовой» вывод установлен слева, а «минусовой» — справа на верхней крышке корпуса АКБ.
Ее особенность заключается в том, что «плюсовой» вывод установлен слева, а «минусовой» — справа на верхней крышке корпуса АКБ. - Обратная полярность – противоположность прямой. Ее используют в европейских странах, поэтому на иномарках применяется именно она. У такой полярности «плюс» расположен справа, а «минусовой» вывод – слева.
Сразу отметим, что и не на всех европейских машинах устанавливаются АКБ с обратной полярностью. Некоторые модели, которые собираются в СНГ, могут комплектоваться аккумуляторами с прямой полярность. А вот на отечественных машинах, даже на самых последних моделях, используются батареи с прямой полярностью.
Теперь о том, почему так важно знать, какая полярность АКБ нужна. Здесь все просто – провода для подключения к батарее имеют ограниченную длину, поэтому установка аккумулятора с неподходящей полярностью приведет к тому, что его просто невозможно будет подключить к бортовой сети, поскольку клеммы не будут доставать до выводов.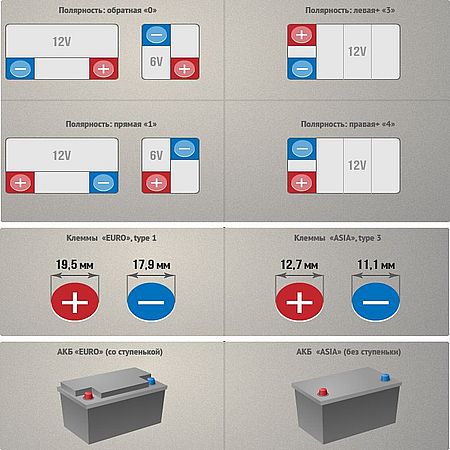
Как определить прямая или обратная?
Распознать, какая полярность у аккумулятора совсем несложно. Достаточно повернуть его «лицом» к себе, то есть, чтобы боковая наклейка была обращена в вашу сторону, а сами выводы располагались с ближней стороны. После этого просто смотрим, как расположены выводы: если «плюс» — слева, то прямая полярность, правое же его положение указывает на обратную.
Но перед приобретением новой батареи важно учитывать не только полярность, но и само ее расположение в посадочном месте на авто. Ведь достаточно повернуть батарею на 180 град, чтобы поменять полярность аккумулятора, вот только выводы в таком случае будут с дальней стороны. А это уже может создать проблемы с подключением АКБ к бортовой сети, из-за того, что проводов будет нахватать или же что-то помешает накинуть и закрепить клеммы.
Видео о прямой и обратной полярности аккумулятора
Что делать если перепутал полярность?
Бывает так, что батарея уже приобретена, но полярность ее не подходит, а возможности заменить на аккумулятор с нужным положением выводов нет.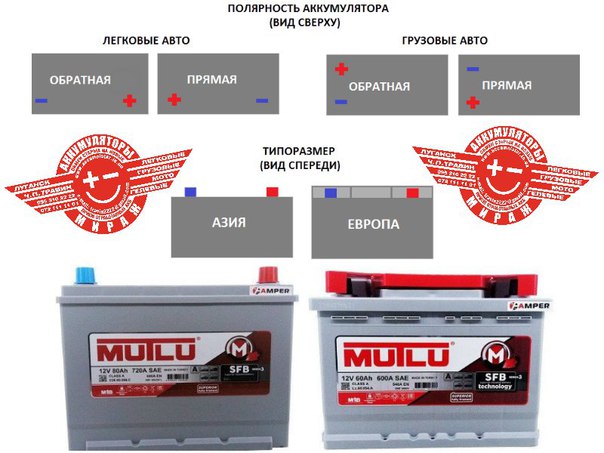 И все же ее можно подключить к сети авто.
И все же ее можно подключить к сети авто.
Но для этого АКБ следует разместить так, чтобы «плюсовой» вывод располагался как можно ближе соответствующей клемме проводки (развернуть аккумулятор, немного сместить его в сторону). Важно сделать так, чтобы получилось подключить клемму к выводу батареи и закрепить ее.
Естественно, «минусовой» провод при этом доставать до вывода не будет, да это и не нужно. Далее берем длинный отрезок провода с хорошим сечением (можно использовать часть провода для «прикуривания»). Откручиваем «родной» массовый провод от кузова авто и заменяем его подготовленным отрезком. Закрепляем на конце клемму для подключения к АКБ и накидываем ее на вывод. Таким способом можно подключить к бортовой сети батарею с любой полярностью.
Похожие публикации
что такое прямая и обратная, в чем разница и как определить отличия
Каждая аккумуляторная батарея имеет на корпусе полюсные выводы – минус (-) и плюс (+). Через клеммы она подключается к бортовой сети автомобиля, питает стартер и другие потребители.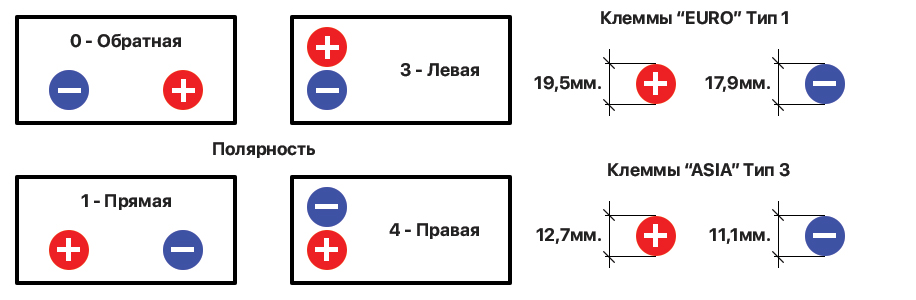 Расположение плюса и минуса определяет полярность АКБ. Водителям важно точно знать полярность аккумулятора, чтобы не перепутать контакты при установке.
Расположение плюса и минуса определяет полярность АКБ. Водителям важно точно знать полярность аккумулятора, чтобы не перепутать контакты при установке.
Полярность аккумулятора
Полярностью называют схему расположения токовыводящих элементов на верхней крышке или лицевой стороне аккумулятора. Другими словами, это положение плюса и минуса. Токовыводы также выполнены из свинца, как и пластины внутри.
Прямая и обратная полярностиСуществуют две распространенные схемы расположения:
- прямая полярность;
- обратная полярность.
Прямая
В советский период все аккумуляторы отечественного производства были с прямой полярностью. Полюсные выводы располагаются по схеме – плюс (+) слева и минус (-) справа. Аккумуляторы с такой же схемой выпускаются и сейчас в России и на постсоветском пространстве. АКБ иностранного производства, которые сделаны в России, также имеют данную схему расположения выводов.
Обратная
На таких аккумуляторах слева расположен минус, а справа плюс. Данное расположение характерно для АКБ европейского производства и поэтому такую полярность часто называют «европолярностью».
Данное расположение характерно для АКБ европейского производства и поэтому такую полярность часто называют «европолярностью».
Каких-то особых преимуществ разная схема положения не дает. Она не влияет на конструкцию и эксплуатационные особенности. Проблемы могут возникнуть при установке нового аккумулятора. Другая полярность заставит поменять положение батареи и длины провода может не хватить. Также водитель может просто перепутать контакты, что приведет к замыканию. Поэтому важно уже при покупке определиться с типом АКБ для своего автомобиля.
Как определить?
Узнать это не так сложно. Для начала нужно повернуть батарею лицевой стороной к себе. Она находится со стороны расположения наклеек с характеристиками и логотипом. Также и полюсные выводы находятся ближе к лицевой стороне.
На многих аккумуляторах можно сразу увидеть знаки «+» и «−», которые точно указывают полярность контактов. Другие производители указывают информацию в маркировке или выделяют токовыводы цветом.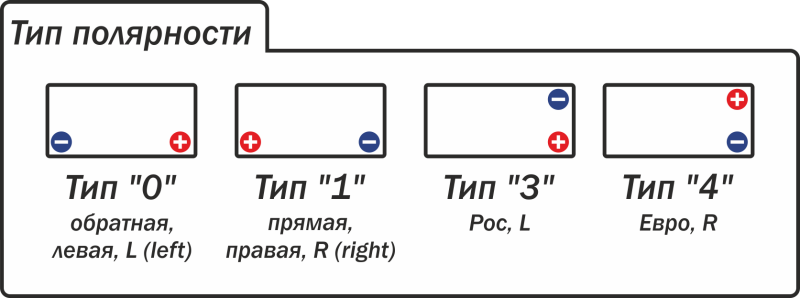 Обычно плюс имеет красный цвет, а минус синий или черный.
Обычно плюс имеет красный цвет, а минус синий или черный.
youtube.com/embed/E1CB-BOOlVo?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>В маркировке обратная полярность обозначается литерой «R» или «0», а прямая литерой – «L» или «1».
Различия в корпусе
Все АКБ можно условно разделить на:
- отечественные;
- европейские;
- азиатские.
Они имеют свои стандарты производства и расположения выводов. Европейские АКБ, как правило, более эргономичны и компактны. Выводные контакты имеют больший диаметр. Плюс – 19,5 мм, минус – 17,9 мм. Диаметр контактов на азиатских АКБ значительно меньше. Плюс – 12,7 мм, минус – 11,1 мм. Это также нужно учитывать. Разность диаметров также указывает на тип полярности.
Можно ли установить аккумулятор другой полярности?
Такой вопрос часто возникает у тех, кто по невнимательности купил аккумулятор другого типа. Теоретически, это возможно, но потребует затрат и лишней волокиты с установкой. Дело в том, что если купить АКБ с обратной полярностью на отечественный автомобиль, то может банально не хватить длины проводов.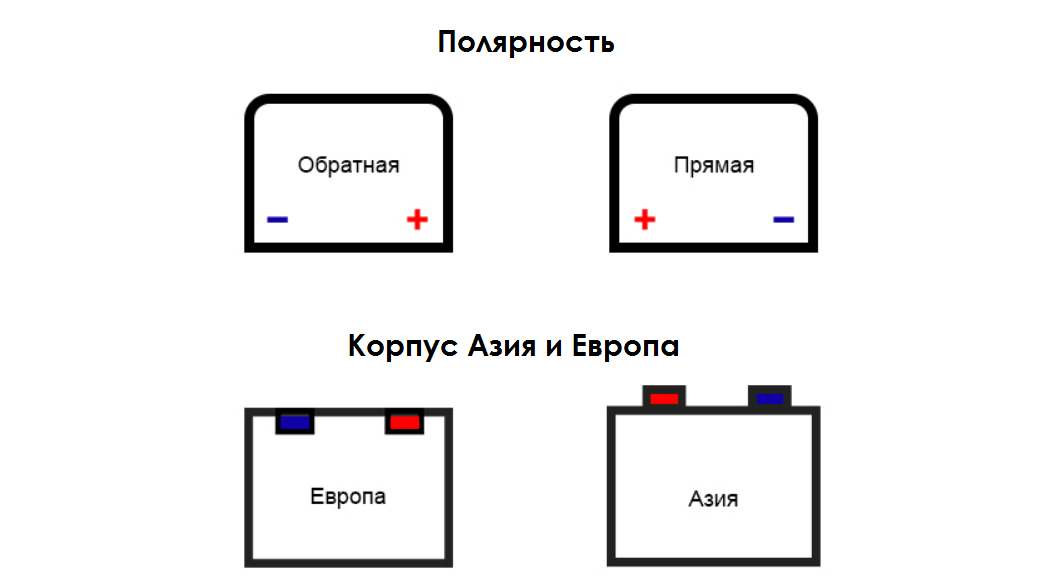 Просто так удлинить провод не получится. Нужно учитывать сечение и диаметр клемм. Также это может сказаться на качестве передачи тока от батареи.
Просто так удлинить провод не получится. Нужно учитывать сечение и диаметр клемм. Также это может сказаться на качестве передачи тока от батареи.
Оптимальным вариантом станет замена аккумулятора на другой с подходящим расположением контактов. Можно попытаться продать купленный АКБ, чтобы не быть в убытке.
Смена полярности аккумулятора
Некоторые водители прибегают к способу переполюсовки АКБ. Эта процедура смены местами плюса и минуса. Также она делается для восстановления работоспособности батареи. Проводить переполюсовку рекомендуется только в крайних случаях.
Внимание! Мы не рекомендуем проводить данную процедуру самостоятельно (без помощи профессионалов) и в необорудованных специальным образом условиях. Последовательность действий ниже приведена в качестве примера, а не инструкции и с целью полноты раскрытия темы статьи.
Последовательность переполюсовки:
- Разрядить батарею до нуля, подключив какую-нибудь нагрузку.

- Плюсовой провод подключить к минусу, а минусовой к плюсу.
- Начать зарядку аккумулятора.
- Прекратить зарядку при закипании банок.
В процессе начнет расти температура. Это нормальное явление, которое указывает на смену полюсов.
Эту процедуру можно проводить только на исправной батарее, которая может выдержать активную сульфатацию. В дешевых АКБ свинцовые пластины очень тонкие, поэтому они могут просто разрушиться и не восстановиться. Также перед началом смены полюсов нужно проверить плотность электролита и банки на замыкание.
Что может произойти, если перепутать при установке?
Если перепутать полярность, то может произойти следующее:
- перегорание предохранителей, реле и проводов;
- выход из строя диодного моста генератора;
- перегорание электронного блока управления двигателем, сигнализации.
Самой простой и дешевой проблемой может стать перегорание предохранителей. Впрочем, это их главная функция. Найти сгоревший предохранитель можно мультиметром путем «прозвона».
Если перепутать контакты, то генератор, наоборот, потребляет энергию от аккумулятора, а не дает ее. Обмотка генератора не рассчитана на входящее напряжение. АКБ также может пострадать и выйти из строя. Самым простым вариантом станет сгорание нужного предохранителя или реле.
Большой проблемой может быть выход из строя электронного блока управления двигателем (ЭБУ). Это устройство требует соблюдения полярности, несмотря на встроенную защиту. Если предохранитель или реле не успеет перегореть, то с большой вероятностью ЭБУ выйдет из строя. Это значит, что автовладельца гарантированно ждет дорогостоящая диагностика и ремонт.
Большинство устройств в электросети автомобиля, такие как автомагнитола или усилитель, имеют защиту от смены полюсов. В их микросхемах предусмотрены специальн
Полярность аккумулятора — что означает и как правильно определить полярность?
Полярность – расположение на крышке аккумулятора присоединительных клемм, которые являются токовыводящими элементами.(2)(1).jpg) Так как полюса всего два – положительный и отрицательный, то и вариантов расположения их немного – прямое и обратное. Мы рассмотрим по отношению к чему принято определять расположение клемм, что будет если случайно перепутать полюса, когда специально делается переполюсовка.
Так как полюса всего два – положительный и отрицательный, то и вариантов расположения их немного – прямое и обратное. Мы рассмотрим по отношению к чему принято определять расположение клемм, что будет если случайно перепутать полюса, когда специально делается переполюсовка.
Что означает прямая и обратная полярность аккумулятора
Расположение клемм на аккумуляторе происходит всегда в определенной последовательности, по стандарту стран производителей. Клеммы всего две, плюс и минус. Они могут иметь разное положение, но наиболее удобным для обслуживания оказалось вынести клеммы на крышку. При этом они бывают поднятыми или утопленными, отличая европейский и азиатский тип.
Клеммы удобно располагать на крышке с двух сторон. Прямая и обратная полярность отличают аккумуляторы только переменой места полюсов. Если прямым считают положение, когда ты читаешь надписи на лицевой стороне, а правая рука касается правой плюсовой кнопки. Обратное положение- та же рука касается отрицательной кнопки.
Это важно учитывать, покупая аккумулятор взамен старого. Подключать клеммы наоборот будет неудобно, придется наращивать один провод, укорачивать другой.
Как определить – полярность аккумулятора прямая или обратная
У каждого аккумулятора есть лицевая сторона, снабженная маркетинговыми и информационными наклейками. Если поставить аккумулятор лицом к себе, клеммы располагаются по правую и левую руку.
«Прямая» полярность в маркировке иногда отмечается цифрой 1. Это российская компоновка аккумуляторов. Если аккумулятор стоит лицом, плюсовая кнопка под левой рукой, красная или с рифленым плюсом. Правая — отрицательная
«Обратная» полярность в классификациях отмечается цифрой «0». Чтобы определиться, нужно поставить аккумулятор лицом к себе. Левая рука ляжет на отрицательную клемму, а правая – на положительную.
Прямая и обратная полярность обозначают различие во внутренней схеме контактов банок на ту или другую сторону. Практически это значит, при замене аккумулятора владелец может перепутать полюса при подключении к шинам авто.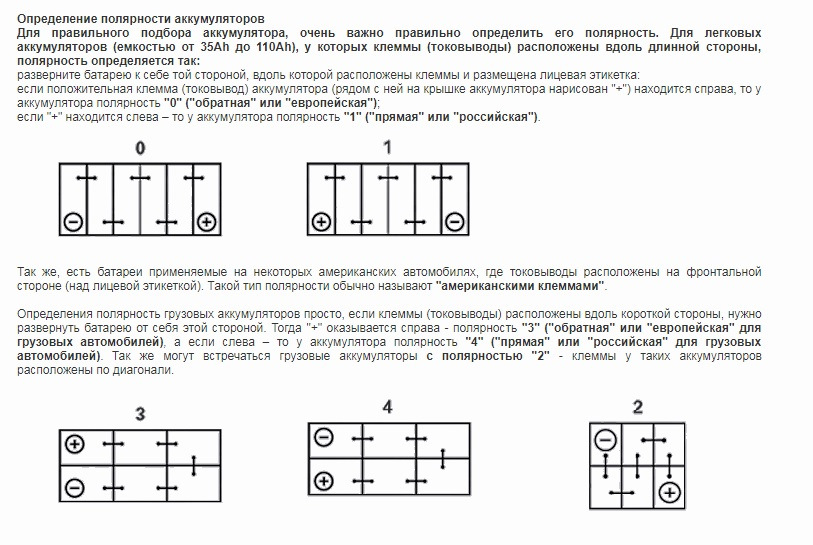
Разница между прямой и обратной полярностью аккумулятора
Ничем другим, кроме расположения полюсов, прямые и обратные схемы соединения банок в батарею не отличаются. Но при установке в гнездо не того аккумулятора могут возникнуть проблемы. Их будет еще больше, если не подойдут провода или перепутаете полярность.
Полярность грузовых аккумуляторов
Конечно, лучше поставить аккумулятор правильной полярности, но места под капотом больше, провода длиннее, поэтому правильно подсоединить можно любой аккумулятор. Важно не перепутать полюса при сборке схемы. В связи с тем что аккумуляторы для грузовиков габаритнее, вариантов подсоединения в них больше — полюса располагаются по вертикали, горизонтали и диагонали, меняясь местами.
Как определить полярность аккумулятора
На грузовых авто установлены емкие и тяжелые аккумуляторы. У них точно также как определяется прямая и обратная полярность. Справа положительный полюс – прямая полярность, отрицательный – обратная.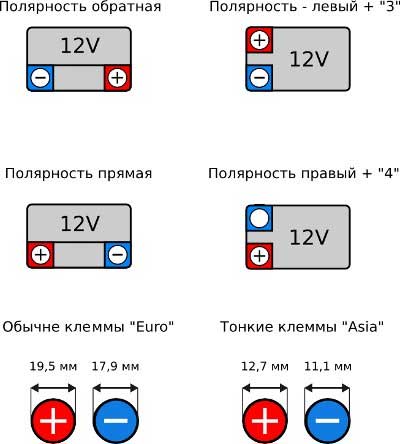 Только смотреть нужно не с лица, а со стороны, где ближе выводы. И обратная полярность в грузовом авто маркируется цифрой «3», а прямая цифрой «4». Если контакты расположились по диагонали – они маркируются цифрой «2». Есть еще виды расположения полюсов с маркировкой «9» и «6»
Только смотреть нужно не с лица, а со стороны, где ближе выводы. И обратная полярность в грузовом авто маркируется цифрой «3», а прямая цифрой «4». Если контакты расположились по диагонали – они маркируются цифрой «2». Есть еще виды расположения полюсов с маркировкой «9» и «6»
Что означает обратная полярность аккумулятора
Обратная полярность значит предусмотрена вариативность посадки – относительное расположение полюсов аккумуляторов даже у одного производителя может быть прямым и обратным. Это позволяет эффективнее использовать подкапотное пространство, делая удобную компоновку. Тем важнее выбрать точно такой же аккумулятор. Если полярность обратная, независимо, в грузовой или легковой машине, катод будет всегда находиться под правой рукой, при условии, что аккумулятор стоит правильно.
Смена полярности аккумулятора
Смена полярности аккумулятора может произойти случайно или преднамеренно. Если вы перепутали клеммы при прикуривании – материальные издержки как донору, так и акцептору обеспечены.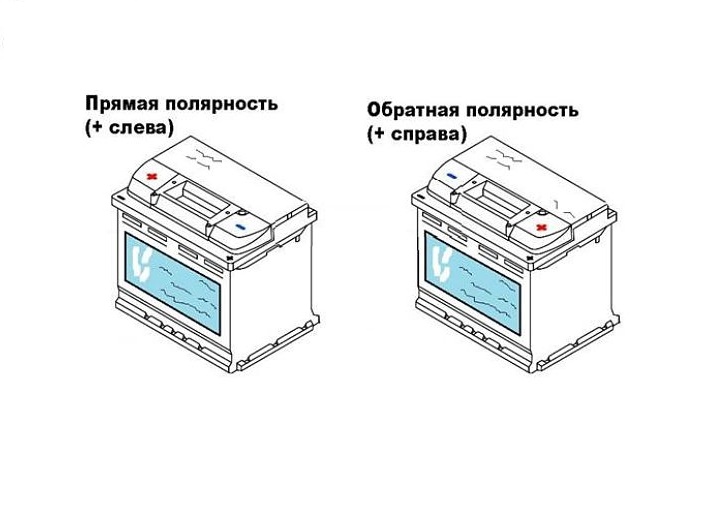
Если случайно произвели смену полярности в своем авто, то в лучшем случае сгорит главный предохранитель, в худшем – диодный мост. Чем быстрее заметили косяк – тем меньше потери.
Смена полярности, как переполюсовка применяется для возвращения работоспособности сульфатированному АКБ. Аккумулятор с аппетитом ест сульфат свинца, очищая пластины. Но переполюсовка – работа аккумулятора вопреки правилам. Вынужденная мера должна быть временной. Гораздо лучше использовать при десульфатации двойную смену полярности.
Видео
Полярность прямая, обратная – вроде бы ясно все. Но случаются эксцессы. Предлагаем видео по теме.
Разница между прямым и обратным смещением по сравнительной таблице
Одно из основных различий между прямым и обратным смещением состоит в том, что при прямом смещении положительная клемма батареи подключается к полупроводниковому материалу p-типа , а отрицательная клемма подключается к n- Тип полупроводниковый материал . В то время как при обратном смещении материал n-типа подключается к положительной клемме источника питания, а материал p-типа подключается к отрицательной клемме батареи.Прямое и обратное смещение дифференцируются ниже в сравнительной таблице.
В то время как при обратном смещении материал n-типа подключается к положительной клемме источника питания, а материал p-типа подключается к отрицательной клемме батареи.Прямое и обратное смещение дифференцируются ниже в сравнительной таблице.
Смещение означает, что к полупроводниковому устройству подключено электрическое питание или разность потенциалов. Разность потенциалов бывает двух типов: прямое смещение и обратное смещение.
Прямое смещение снижает потенциальный барьер диода и обеспечивает легкий путь для прохождения тока. В то время как в обратное смещение разность потенциалов увеличивает силу барьера, который не позволяет носителю заряда перемещаться через переход.Обратное смещение обеспечивает высокий резистивный путь для прохождения тока, и, следовательно, ток не течет через цепь.
Содержание: прямое смещение по сравнению с обратным смещением
- Сравнительная таблица
- Определение
- Ключевые отличия
Сравнительная таблица
| Основа для сравнения | Прямое смещение | Обратное смещение |
|---|---|---|
| Определение | Внешнее напряжение, которое прикладывается к PN-диоду для уменьшения потенциального барьера и образует легкий ток через него, называется прямым смещением. | Внешнее напряжение, которое прикладывается к PN-переходу для усиления потенциального барьера и предотвращает прохождение тока через него, называется обратным смещением. |
| Символ | ||
| Подключение | Положительная клемма батареи подключена к полупроводнику P-типа устройства, а отрицательная клемма подключена к полупроводнику N-типа | Отрицательная клемма батареи подключена к P-области и положительный полюс батареи подключен к полупроводнику N-типа. |
| Барьерный потенциал | Снижает | Усиление |
| Напряжение | Напряжение анода больше, чем катода. | Напряжение на катоде больше, чем на аноде. |
| Прямой ток | Большой | Маленький |
| Слой истощения | Тонкий | Толстый |
| Сопротивление | Низкое | Высокое |
| Текущий поток | Допускает | Предотвращает |
| Величина тока | Зависит от прямого напряжения. | Ноль |
| Эксплуатация | Проводник | Изолятор |
Определение прямого смещения
При прямом смещении внешнее напряжение подается на диод PN-перехода. Это напряжение устраняет потенциальный барьер и обеспечивает путь с низким сопротивлением для прохождения тока. Прямое смещение означает, что положительная область подключена к p-клемме источника питания, а отрицательная область подключена к n-типу устройства.
Напряжение потенциального барьера очень мало (около 0,7 В для кремния и 0,3 В для германиевого перехода), поэтому для полного устранения барьера требуется очень небольшое напряжение. Полное устранение барьера составляет путь с низким сопротивлением для прохождения тока. Таким образом, через переход начинает течь ток. Этот ток называется прямым током.
Определение обратного смещения
При обратном смещении отрицательная область подключена к положительной клемме батареи, а положительная область подключена к отрицательной клемме. Обратный потенциал увеличивает силу потенциального барьера. Потенциальный барьер препятствует потоку носителей заряда через переход. Это создает путь с высоким сопротивлением, в котором ток не течет через цепь.
Обратный потенциал увеличивает силу потенциального барьера. Потенциальный барьер препятствует потоку носителей заряда через переход. Это создает путь с высоким сопротивлением, в котором ток не течет через цепь.
Ключевые различия между прямым и обратным смещением
- Прямое смещение снижает силу потенциального барьера, из-за чего ток легко проходит через переход, тогда как обратное смещение усиливает потенциальный барьер и препятствует потоку носителей заряда.
- При прямом смещении положительный полюс батареи подключается к p-области, а отрицательный вывод подключается к материалу n-типа, в то время как при обратном смещении положительный вывод источника питания подключается к материалу n-типа, а отрицательный клемма подключается к материалу p-типа устройства.
- Прямое смещение создает электрическое поле поперек потенциала, которое снижает силу потенциального барьера, тогда как обратное смещение увеличивает силу потенциального барьера.
- Примечание.
 Потенциальный барьер — это слой между диодом с PN-переходом, который ограничивает движение электронов через переход.
Потенциальный барьер — это слой между диодом с PN-переходом, который ограничивает движение электронов через переход.
- Примечание.
- При прямом смещении напряжение на аноде больше, чем на катоде, тогда как при обратном смещении напряжение на катоде больше, чем на аноде.
- Прямое смещение имеет большой прямой ток, а обратное смещение имеет очень маленький прямой ток.
- Примечание. Ток в диоде, когда он течет в прямом направлении, называется прямым током.
- Слой обеднения диода очень тонкий при прямом смещении и толстый при обратном смещении.
- Примечание. Слой обеднения — это область вокруг соединения, в которой свободные носители заряда истощены.
- Прямое смещение уменьшает сопротивление диода, тогда как обратное смещение увеличивает сопротивление диода.
- При прямом смещении ток легко течет по цепи, тогда как обратное смещение не позволяет току проходить через нее.
- При прямом смещении величина тока зависит от прямого напряжения, тогда как при обратном смещении величина тока очень мала или незначительна.

- При прямом смещении устройство работает как проводник, тогда как при обратном смещении устройство действует как изолятор.
Прямое напряжение кремниевого диода составляет 0,7 В, а прямое напряжение германия — 0,3 В.
.Схема защиты от обратной полярностис использованием диода ИЛИ МОП-транзистора с P-каналом
Батареи являются наиболее удобным источником питания для подачи напряжения на электронную схему. Есть много других способов питания электронных устройств, таких как адаптер, солнечная батарея и т. Д., Но наиболее распространенным источником питания постоянного тока является аккумулятор. Как правило, все устройства поставляются со схемой защиты от обратной полярности , но если у вас есть какое-либо устройство с батарейным питанием, которое не имеет защиты от обратной полярности, вы всегда должны быть осторожны при замене батареи, иначе она может взорвать устройство.
Итак, в этой ситуации Схема защиты от обратной полярности была бы полезным дополнением к схеме.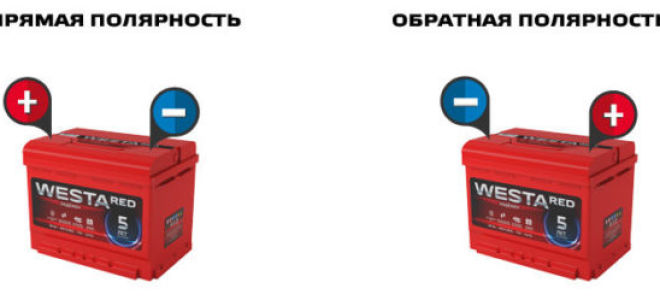 Существует несколько простых методов защиты схемы от подключения с обратной полярностью, например, использование диода или диодного моста или использование полевого МОП-транзистора с каналом P в качестве переключателя на ВЫСОКОЙ стороне.
Существует несколько простых методов защиты схемы от подключения с обратной полярностью, например, использование диода или диодного моста или использование полевого МОП-транзистора с каналом P в качестве переключателя на ВЫСОКОЙ стороне.
Использование диода — самый простой и дешевый метод защиты от обратной полярности, но он имеет проблему утечки мощности .Когда входное напряжение питания высокое, небольшое падение напряжения может не иметь значения, особенно при низком токе. Но в случае низковольтной операционной системы недопустимо даже небольшое падение напряжения.
Как мы знаем, падение напряжения на диоде общего назначения составляет 0,7 В, поэтому мы можем ограничить это падение напряжения с помощью диода Шоттки, поскольку его падение напряжения составляет примерно 0,3–0,4 В, и он также может выдерживать большие токовые нагрузки. Имейте в виду, выбирая диод Шоттки, поскольку многие диоды Шоттки имеют высокую утечку обратного тока, поэтому убедитесь, что вы выберете диод с низким обратным током (менее 100 мкА).
При 4 А потери мощности на диоде Шоттки в цепи будут:
4 x 0,4 Вт = 1,6 Вт
А в обычном диоде:
4 x 0,7 = 2,8 Вт.
Вы можете даже использовать мостовой выпрямитель для защиты от обратной полярности, независимо от полярности. Но мостовой выпрямитель состоит из четырех диодов, следовательно, количество потерь энергии будет вдвое больше, чем в приведенной выше схеме с одним диодом.
Защита от обратной полярности с использованием P-канального MOSFET Использование полевого МОП-транзистора с каналом P для защиты от обратной полярности более надежно, чем другие методы, из-за низкого падения напряжения и высоких токов.Схема состоит из P-канального МОП-транзистора, стабилитрона и понижающего резистора. Если напряжение питания меньше, чем напряжение затвор-исток (Vgs) P-канального MOSFET, вам понадобится только MOSFET без диода или резистора. Вам просто нужно подключить клемму затвора полевого МОП-транзистора к земле.
Теперь, если напряжение питания больше, чем Vgs, вам нужно понизить напряжение между выводом затвора и истоком. Компоненты, необходимые для изготовления аппаратной части схемы, упомянуты ниже.
Необходимые материалы- FQP47P06 МОП-транзистор с P-каналом
- Резистор (100к)
- Стабилитрон 9,1 В
- Макет
- Соединительные провода
Теперь, когда вы подключаете батарею в соответствии с принципиальной схемой с правильной полярностью, это приводит к включению транзистора и пропусканию тока через него.Если батарея подключена в обратном направлении или с обратной полярностью, транзистор выключается, и ваша схема становится защищенной.
Эта схема защиты более эффективна, чем другие. Давайте проанализируем схему , когда батарея подключена правильно..jpg) , P-канальный MOSFET включится, потому что напряжение между затвором и истоком отрицательное. Формула для определения напряжения между затвором и истоком:
, P-канальный MOSFET включится, потому что напряжение между затвором и истоком отрицательное. Формула для определения напряжения между затвором и истоком:
Vgs = (Vg - Vs)
Когда батарея подключена неправильно , напряжение на выводе затвора будет положительным, и мы знаем, что P-Channel MOSFET включается только тогда, когда напряжение на выводе затвора отрицательное (минимум -2.0 В для этого полевого МОП-транзистора или меньше). Таким образом, всякий раз, когда батарея подключается в обратном направлении, цепь будет защищена полевым МОП-транзистором.
Теперь давайте поговорим о потере мощности в схеме , когда транзистор включен, сопротивление между стоком и истоком почти ничтожно, но для большей точности вы можете просмотреть данные P-канального MOSFET. Для P-канального МОП-транзистора FQP47P06 статическое сопротивление сток-исток во включенном состоянии (R DS (ON) ) составляет 0,026 Ом (макс. ).Итак, мы можем рассчитать потери мощности в цепи, как показано ниже:
).Итак, мы можем рассчитать потери мощности в цепи, как показано ниже:
Потери мощности = I 2 R
Предположим, ток, протекающий через транзистор, составляет 1 А. Значит потеря мощности будет
Потери мощности = I 2 R = (1A) 2 * 0,026 Ом = 0,026 Вт
Следовательно, потери мощности примерно в 27 раз меньше, чем в схеме с одним диодом. Вот почему использование P-канального MOSFET для защиты от обратной полярности намного лучше, чем другие методы.Он немного дороже диода, но делает схему защиты более безопасной и эффективной.
Мы также использовали стабилитрон и резистор в схеме для защиты от превышения напряжения затвор-исток. Добавив резистор и стабилитрон на 9,1 В, мы можем ограничить напряжение затвор-исток максимум до отрицательного значения 9,1 В, поэтому транзистор остается безопасным.
.Понимание основ многоадресной рассылки RPF (пересылка обратного пути)
Введение:При нормальной маршрутизации, то есть при одноадресной маршрутизации решения о пересылке пакетов обычно основываются на адресе назначения пакета, поступающего на маршрутизатор. Таблица одноадресной маршрутизации организована по подсети назначения и в основном настроена для пересылки пакета к месту назначения.
При многоадресной IP-маршрутизации маршрутизатор пересылает пакет от источника для продвижения по дереву распределения и предотвращения петель маршрутизации.Состояние многоадресной пересылки маршрутизатора работает более логично за счет организации таблиц на основе обратного пути от получателя обратно к корню дерева распределения. Этот процесс известен как пересылка по обратному пути (RPF).
Короче говоря, входящий многоадресный пакет не будет принят / переадресован, если он не получен на интерфейсе, который является исходящим интерфейсом для одноадресного маршрута к источнику пакета.
Пример конфигурации:В приведенном ниже примере многоадресный сервер S1 отправляет многоадресный пакет, а R1 лавинно рассылает его R2 и R3.R2 получил свою копию и тоже залил ее. В результате R3 получает один и тот же пакет от двух маршрутизаторов:
a) На своем интерфейсе fa0 / 0 от R1.
б) На его интерфейсе s0 / 0 от R2.
Схема топологии:
Без проверки RPF R3 пересылает полученный пакет от R1 на R2 и наоборот, и начинает процесс зацикливания пакетов с той же логикой, R1 и R2 также продолжайте повторять процесс. Это дублирование создает петли многоадресной маршрутизации и порождает штормы многоадресной рассылки, которые расходуют пропускную способность и ресурсы маршрутизатора.
Прежде чем я углублюсь в настройку многоадресной рассылки, позвольте мне поделиться с вами начальной конфигурацией нашей сети. Все соответствующие конфигурации приведены ниже.
R1
R2
R3
имя хоста R1 ip cef !ip multicast-routing ! интерфейс FastEthernet1 / 0 IP-адрес 1.1.1.1 255.255.255.0 IP pim в плотном режиме ! интерфейс FastEthernet0 / 0 IP-адрес 10.1.1.1 255.255.255.252 IP pim в плотном режиме скорость 100 полнодуплексный интерфейс FastEthernet0 / 1 ip-адрес 10.1.1.5 255.255.255.252 ip pim в плотном режиме скорость 100 полнодуплексный роутер eigrp 1 сеть 1.1.1.1 0.0.0.0 сеть 10.1.1.0 0.0.0.255 нет авто-сводки | имя хоста R2 ! ip multicast-routing ! интерфейс FastEthernet0 / 0 ip-адрес 10.1.1.2 255.255.255.252 ip pim в плотном режиме скорость 100 полнодуплексный интерфейс Serial0 / 0 IP-адрес 10.1.1.9 255.255.255.252 ip pim в плотном режиме тактовая частота 2000000 ! роутер eigrp 1 сеть 10.1.1.0 0.0.0.255 нет авто-сводки ! | имя хоста R3 ! ip cef ! ip multicast-routing ! интерфейс FastEthernet0 / 0 IP-адрес 10.1.1.6 255.255.255.252 ip pim в плотном режиме нет ip route-cache нет ip mroute-cache скорость 100 полнодуплекс ! интерфейс FastEthernet0 / 1 ip-адрес 3.3.3.3 255.255.255.0 ip pim в плотном режиме ip igmp join-group 239.1.1.1 интерфейс Serial0 / 0 IP-адрес 10.1.1.10 255.255.255.252 ip pim в плотном режиме no ip route-cache no ip mroute-cache тактовая частота 2000000 ! роутер eigrp 1 сеть 3.3.3.3 0.0.0.0 сеть 10.1.1.0 0.0.0.255 no auto-summary ! |
Когда R3 выполняет проверку RPF, происходит следующее:
1) R3 проверяет адрес источника каждого входящего пакета, который равен 1.1.1.1.
2) R3 определяет интерфейс обратного пути на основе его маршрута, используемого для пересылки пакетов к 1.1.1.1
В нашем случае маршрут R3 к 1.1.1.1/24 совпадает, и он перечисляет исходящий интерфейс fa0 / 0, что делает fa0 / 0 RPF-интерфейс R3 для IP-адреса 1.1.1.1
R3 # sh ip route | begin Gate
Шлюз последней инстанции не установлен
1.0.0.0/24 разделен на подсети, 1 подсети
D 1.1.1.0 [90/156160] через 10.1.1.5, 02:01:51, FastEthernet0 / 0
3.0.0.0 / 24 разделен на подсети, 1 подсеть
C 3.3.3.0 подключена напрямую, Loopback0
10.0.0.0/30 разделена на подсети, 3 подсети
C 10.1.1.8 подключено напрямую, Serial0 / 0
D 10.1 .1.0 [90/30720] через 10.1.1.5, 04:24:40, FastEthernet0 / 0
C 10.1.1.4 подключен напрямую, FastEthernet0 / 0
R3 # sh ip rpf 1.1.1.1
Информация RPF за ? (1.1.1.1)
Интерфейс RPF: FastEthernet0 / 0
Сосед RPF:? (10.1.1.5)
Маршрут / маска RPF: 1.1.1.0/24
Тип RPF: одноадресная (eigrp 1)
Количество рекурсий RPF: 0
Выполнение поиска по таблицам с предпочтительным расстоянием
R3 # sh ip mroute | Beg Interfac
Состояние интерфейса: Интерфейс, Следующий переход или VCD, Состояние / режим
(*, 239.1.1.1), 00: 38: 46 / остановлено, RP 0.0.0.0, флаги: DCL
Входящий интерфейс : Null, RPF nbr 0.0.0.0
Список исходящих интерфейсов:
Loopback0, Forward / Dense, 00: 38: 46/00: 00: 00
FastEthernet0 / 0, Forward / Dense, 00: 38: 46/00 : 00: 00
Serial0 / 0, Forward / Dense, 00: 38: 46/00: 00: 00
(1.1.1.1, 239.1.1.1), 00: 00: 26/00: 02: 37, флаги: LT
Входящий интерфейс: FastEthernet0 / 0, RPF nbr 10.1.1.5
Список исходящих интерфейсов:
Loopback0, Forward / Dense, 00: 00: 26/00: 00: 00
Serial0 / 0, Prune / Dense, 00: 00: 26/00: 02: 34, A
3) R3 сравнивает интерфейс обратного пути fa0 / 0, на который приходит многоадресный пакет. Если они совпадают, он принимает пакеты и пересылает их; в противном случае он отбрасывает пакет. В этом случае R3 лавинно рассылает пакеты, полученные на fa0 / 0 от R1, но игнорирует пакеты, полученные на s0 / 0 от R2.
Проверка:1) Чтобы проверить, мы будем отправлять эхо ICMP группе 239.1.1.1 с R1 с источником 1.1.1.1. Всегда безопасно собирать журналы отладки в буфере, а не на консоли, поэтому мы будем отлаживать многоадресную рассылку пакет и соберите его в буфере регистрации, как показано ниже:
R3 # conf t
Введите команды конфигурации, по одной в каждой строке. Закончите CNTL / Z.
R3 (config) # информация консоли журналов
R3 (config) #logging buffer 7
R3 (config) #logging buffer 64000
R3 (config) #no ip cef
R3 (config) #end
* 1 марта, 04:44:41.670:% SYS-5-CONFIG_I: Настраивается с консоли с помощью консоли
R3 # debug ip mpacket
Отладка многоадресных IP-пакетов выполняется
R1 # ping 239.1.1.1 source 1.1.1.1
Тип escape-последовательность чтобы прервать.
Отправка 1, 100-байтового эха ICMP на 239.1.1.1, тайм-аут составляет 2 секунды:
Пакет отправлен с адресом источника 1.1.1.1
Ответ на запрос 0 из 10.1.1.6, 24 мс
Ответ запросить 0 из 10.1.1.6, 128 мс
R3 # sh logging | begin Log
Буфер журнала (64000 байт):
IP (0): s = 10.1.1.5 (FastEthernet0 / 0) d = 239.1.1.1 (Serial0 / 0) id = 19, ttl = 254, prot = 1, len = 100 (100), mforward
IP (0): s = 10.1.1.1 (Serial0 / 0) d = 239.1.1.1 id = 19, ttl = 253, prot = 1, len = 104 (100) , не интерфейс RPF
IP (0): s = 10.1.1.5 (FastEthernet0 / 0) d = 239.1.1.1 (Serial0 / 0) id = 20, ttl = 254, prot = 1, len = 100 (100), mforward
IP (0): s = 10.1.1.1 (Serial0 / 0) d = 239.1.1.1 id = 20, ttl = 253, prot = 1, len = 104 (100), не интерфейс RPF
IP (0): s = 1.1.1.1 (FastEthernet0 / 0) d = 239.1.1.1 (Serial0 / 0) id = 20, ttl = 253, prot = 1, len = 100 (100), mforward
IP (0): s = 1.1.1.1 (Serial0 / 0) d = 239.1.1.1 id = 20, ttl = 252, prot = 1, len = 104 (100), не интерфейс RPF
Из приведенных выше журналов мы видим, что R3 перенаправил пакеты, полученные на fa0 / 0 от R1, но игнорирует пакеты, полученные на s0 / 0 от R2.
2) Давайте посмотрим на то же самое с mtrace от R1 и захватом пакета с помощью wirehark на интерфейсах Fa0 / 0 и S0 / 0 R3.
R1 # mtrace 1.1.1.1 3.3.3.3 239.1.1.1
Введите escape-последовательность для отмены.
Mtrace из 1.1.1.1 в 3.3.3.3 через группу 239.1.1.1
От источника (?) До пункта назначения (?)
Запрос полного обратного пути …
0 3.3.3.3
-1 10.1.1.6 PIM [1.1.1.0/24]
-2 10.1.1.5 PIM [1.1.1.0/24]
-3 1.1.1.1
На интерфейсе R3 fa0 / 0 мы фиксируем запрос маршрута и запрос, как указано в черный ящик под диаграммой:
Давайте откроем пакет запроса traceroute, чтобы получить более подробную информацию изнутри.
Как показано на рисунке выше Поле «FORWORDING CODE: NO_ERROR» показывает, что после того, как маршрутизатор получил многоадресный пакет, он выполнил проверку RPF, поскольку проверка RPF прошла успешно, пакет пересылается.
Теперь рассмотрим захват, сделанный на интерфейсе S0 / 0:
Он показывает только запрос трассировки маршрута, а не запрос, поскольку пакеты отбрасываются из-за сбоя проверки RPF.
Отсюда вывод: проверка RPF — это стратегия, с помощью которой маршрутизатор принимает пакеты, которые прибывают по кратчайшему пути, и отбрасывает те, которые прибывают по более длинным маршрутам, и тем самым избегает петель маршрутизации и дублирования.
Связанная информация:IP Multicast
Обзор технологии IP Multicast
Настройка многоадресной IP-маршрутизации
.Прямое распространение в нейронных сетях — Упрощенная математическая и программная версия | автор: викашрадж луханивал
Как мы все знаем из последнего десятилетия глубокое обучение стало одной из наиболее широко распространенных новых технологий. Это связано с его репрезентативной силой функций.
Согласно Универсальная аппроксимационная теорема , хорошо управляемая и спроектированная глубокая нейронная сеть может аппроксимировать любую произвольную сложную и непрерывную связь между переменными.На самом деле, есть несколько других причин успеха глубокого обучения . Я не буду здесь обсуждать эти возможные причины.
Цель этого поста — объяснить прямое распространение (один из основных процессов на этапе обучения) более простым способом.
Обучающий алгоритм / модель определяет параметры (веса и смещения) с помощью прямого распространения , и обратного распространения .
a Как следует из названия, входные данные передаются в прямом направлении по сети.Каждый скрытый слой принимает входные данные, обрабатывает их в соответствии с функцией активации и переходит на следующий уровень.
Почему сеть прямого распространения?
Чтобы сгенерировать какой-либо вывод, входные данные должны подаваться только в прямом направлении. Данные не должны течь в обратном направлении во время генерации выходных данных, в противном случае они будут формировать цикл, и выходные данные никогда не будут созданы. Такие конфигурации сети известны как сеть прямого распространения .Сеть прямого распространения помогает в прямом распространении .
На каждом нейроне в скрытом или выходном слое обработка происходит в два этапа:
- Предварительная активация: это взвешенная сумма входов , т.е. линейное преобразование весов относительно доступных входов. На основе этой агрегированной суммы и функции активации нейрон принимает решение, передавать эту информацию дальше или нет.
- Активация: вычисленная взвешенная сумма входов передается в функцию активации. Функция активации — это математическая функция, которая добавляет сети нелинейность. Существует четыре часто используемых и популярных функции активации — сигмовидная, гиперболический тангенс (tanh), ReLU и Softmax.
Теперь давайте разберемся с прямым распространением на примере. Рассмотрим нелинейно разделяемых данных в виде двух лун точек данных, следующих по спирали.Эти сгенерированные данные имеют два разных класса.
Данные могут быть сгенерированы с помощью функции make_moons () модуля sklearn.datasets . Общее количество сэмплов, которые должны быть сгенерированы, и шум формы луны можно отрегулировать с помощью параметров функции.
import numpy as npвизуализация набора данных
import matplotlib.pyplot as plt
import matplotlib.colors
from sklearn.datasets import make_moonsnp.random.seed (0) data, labels = make_moons (n_samples = 200, noise = 0.04, random_state = 0)
print (data.shape, labels.shape) color_map = matplotlib.colors.LinearSegmentedColormap.from_list ("", ["красный", "желтый"])
plt.scatter (data [:, 0 ], data [:, 1], c = labels, cmap = my_cmap)
plt.show ()
Здесь для генерации данных используются 200 выборок, и у них есть два класса, показанные красным и зеленым цветом.
Теперь давайте посмотрим на структуру нейронной сети, чтобы предсказать класс для этой задачи двоичной классификации . Здесь я собираюсь использовать один скрытый слой с двумя нейронами, выходной слой с одним нейроном и сигмоидальную функцию активации .
Во время прямого распространения на каждом узле скрытого и выходного уровня происходит предварительная активация и активация . Например, в первом узле скрытого уровня сначала вычисляется a1 ( преактивация ), а затем вычисляется h3 ( активация ).
a1 — это взвешенная сумма входов. Здесь веса генерируются случайным образом.
a1 = w1 * x1 + w2 * x2 + b1 = 1.76 * 0,88 + 0,40 * (- 0,49) + 0 = 1,37 приблизительно и h3 — значение функции активации, примененной к a1.
Аналогично
a2 = w3 * x1 + w4 * x2 + b2 = 0,97 * 0,88 + 2,24 * (- 0,49) + 0 = -2,29 приблизительно и
Для любого слоя после первого скрытого слоя ввод вывод из предыдущего слоя.
a3 = w5 * h3 + w6 * h4 + b3 = 1,86 * 0,8 + (-0,97) * 0,44 + 0 = 1,1 приблизительно
и
Таким образом, вероятность того, что первое наблюдение будет принадлежать к классу 1, составляет 74%. .Таким же образом можно рассчитать прогнозируемый результат для всех других наблюдений.
На изображении ниже представлено преобразование данных из входного слоя в выходной слой для первого наблюдения.
Преобразование данных из входного уровня в выходнойТеперь давайте посмотрим, как реализована вышеупомянутая нейронная сеть в блокноте Jupyter. Фактически, при построении глубоких нейронных сетей используются такие фреймворки, как Tensorflow, Keras, PyTorch и т. Д.
из sklearn.model_selection import train_test_split # Разделение данных на данные обучения и тестирования
X_train, X_val, Y_train, Y_val = train_test_split (data, labels, stratify = labels, random_state = 0)
print (X_train.shape, X_val.shape)
Здесь 150 наблюдений используются для целей обучения и 50 для целей тестирования в соответствии с коэффициентом разделения по умолчанию 75:25.
Теперь давайте определим класс для прямого распространения , где веса инициализируются случайным образом.
класс FeedForwardNetwork:def __init __ (self):
np.random.seed (0)
self.w1 = np.random.randn ()
self.w2 = np.random.randn ()
self.w3 = np.random.randn ()
self.w4 = np.random.randn ()
self.w5 = np.random.randn ()
self.w6 = np.random.randn ()
self.b1 = 0
self.b2 = 0
self.b3 = 0def sigmoid (self, x):
return 1.0 / (1.0 + np.exp (-x))def forward_pass (self, x):
self.x1, self.x2 = x
self.a1 = self.w1 * self.x1 + self.w2 * self.x2 + self.b1
self.h3 = self.sigmoid (self.a1)
self.a2 = self.w3 * self.x1 + self.w4 * self.x2 + self.b2
self.h4 = self.sigmoid (self.a2)
self.a3 = self.w5 * self.h3 + self.w6 * self.h4 + self.b3
self.h5 = self.sigmoid (self.a3)
forward_matrix = np.array ([[0,0,0,0, self.h5,0,0,0],
[0,0, (self .w5 * self.h3), (self.w6 * self.h4), self.b3, self.a3,0,0],
[0,0,0, self.h3,0,0,0, self .h4],
[(self.w1 * self.x1), (self.w2 * self.x2), self.b1, self.a1, (self.w3 * self.x1), (self.w4 * self .x2), self.b2, self.a2]])
forward_matrices.append (forward_matrix)
return self.h5
Здесь функция forward_pass () вычисляет выходное значение для данного входного наблюдения. forward_matrix — это 2d-массив для хранения значений a1, h3, a2, h4, a3, h5 и т.д. для каждого наблюдения. Причина его использования — просто визуализировать преобразование этих значений с помощью изображения в формате GIF. Записи forward_matrix показаны ниже
forward_matrices = []
ffn = FeedForwardNetwork ()
для x в X_train:
ffn.forward_pass (x)
forward_matrices — это список forward_matrix для всех наблюдения.
import seaborn as sns
import imageio
from IPython.display import HTMLdef plot_heat_map (Наблюдение):
fig = plt.figure (figsize = (10, 1))
sns.heatmap (forward_matrices [наблюдение], annot = True, cmap = my_cmap, vmin = -3, vmax = 3)
plt.title («Наблюдение» + str (наблюдение)) fig.canvas.draw ()
image = np.frombuffer (fig.canvas.tostring_rgb (), dtype = 'uint8')
image = image.reshape (fig.canvas.get_width_height () [:: - 1] + (3,)) вернуть imageimageio.mimsave ('./ forwardpropagation_viz.gif', [plot_heat_map (i) for i in range (0, len (forward_matrices), len (forward_matrices) // 15)], fps = 1)
plot_heat_map () функция создает тепловая карта для визуализации значений forward_matrix для каждого наблюдения. Эти тепловые карты хранятся в изображении forwardpropagation_viz.gif . Здесь создано 15 различных тепловых карт для 15 различных наблюдений.
Оптимизация кода
Вместо использования разных переменных, таких как w1, w2… w6, a1, a2, h3, h4 и т. Д.отдельно векторизованная матрица может использоваться для весов, предварительной активации (а) и активации (h) соответственно. Векторизация обеспечивает более эффективное и быстрое выполнение кода. Он также имеет простой для понимания синтаксис.
class FeedForwardNetwork_Vectorised:Заключениеdef __init __ (self):
np.random.seed (0)
self.W1 = np.random.randn (2,2)
self.W2 = np.random.randn (2,1 )
self.B1 = np.zeros ((1,2))
self.B2 = np.zeros ((1,1))def sigmoid (self, X):
return 1.0 / (1.0 + np.exp (-X))def forward_pass (self, X):
ffn_v = FeedForwardNetwork_Vectorised ()
self.A1 = np.matmul (X, self.W1) + self.B1
self.h3 = self.sigmoid (self.A1)
self.A2 = np.matmul (self.h3, self.W2) + self.B2
self.h4 = self.sigmoid (self.A2)
return self.h4
ffn_v.forward_pass (X_train)
Это примерно прямое распространение с моей стороны, и я надеюсь, что смог объяснить интуицию и шаги, связанные с прямым распространением .Если вы хотите узнать больше о нейронных сетях, обратитесь к другим моим предложениям блога о нейронных сетях. Ссылки ниже
A comprehensive guide to Feature Selection using Wrapper methods in Python
Почему лучше вес инициализация важна в нейронных сетях?
Анализируем разные типы функций активации в нейронных сетях — какой из них предпочесть?
Почему градиентного спуска недостаточно: всестороннее введение в алгоритмы оптимизации в нейронных сетях
.Нейронная сеть с кодированием— прямое и обратное распространение | Имад Даббура
Почему нейронные сети?
Согласно универсальной приближенной теореме , нейронные сети могут приближать, а также изучать и представлять любую функцию с учетом достаточно большого слоя и желаемой погрешности. Нейронная сеть узнает истинную функцию путем построения сложных представлений поверх простых. На каждом скрытом слое нейронная сеть изучает новое пространство признаков, сначала вычисляя аффинные (линейные) преобразования заданных входных данных, а затем применяя нелинейную функцию, которая, в свою очередь, будет входом следующего слоя.Этот процесс будет продолжаться, пока мы не дойдем до выходного слоя. Следовательно, мы можем определить нейронную сеть как поток информации от входов через скрытые слои к выходу. Для трехуровневой нейронной сети изученная функция будет: f (x) = f_3 (f_2 (f_1 (x))) где:
- f_1 (x) : функция, изученная на первом скрытом слое
- f_2 (x) : функция, изученная на втором скрытом слое
- f_3 (x) : функция, изученная на выходном слое
Таким образом, на каждом слое мы изучаем разное представление, которое усложняется с последующими скрытыми слоями.Ниже приведен пример трехуровневой нейронной сети (входной слой не считается):
Рисунок 1: Нейронная сеть с двумя скрытыми слоямиНапример, компьютеры не могут понимать изображения напрямую и не знают, что делать с данными пикселей. Однако нейронная сеть может построить простое представление изображения на ранних скрытых слоях, которое идентифицирует края. Получив первый вывод скрытого слоя, он может изучить углы и контуры. Учитывая второй скрытый слой, он может изучить такие части, как нос.Наконец, он может узнать идентичность объекта.
Поскольку истина никогда не бывает линейной и представление очень важно для производительности алгоритма машинного обучения, нейронная сеть может помочь нам построить очень сложные модели и предоставить алгоритму изучение таких представлений, не беспокоясь о проектировании функций, которое требует специалистов-практиков. очень много времени и усилий, чтобы создать хорошее представление.
Сообщение состоит из двух частей:
- Кодирование нейронной сети: это влечет за собой написание всех вспомогательных функций, которые позволили бы нам реализовать многоуровневую нейронную сеть.При этом я буду объяснять теоретические части, когда это возможно, и давать несколько советов по реализации.
- Приложение: мы реализуем нейронную сеть, которую мы закодировали в первой части по проблеме распознавания изображений, чтобы увидеть, сможет ли созданная нами сеть определить, есть ли на изображении кошка или собака, и увидеть, как она работает 🙂
Этот пост будет первым в серии постов, посвященных реализации нейронной сети в numpy, включая проверку градиента , инициализацию параметров, регуляризацию L2, выпадение .. Архитектура сети влечет за собой определение ее глубины, ширины и функций активации, используемых на каждом уровне. Глубина — количество скрытых слоев. Ширина — это количество единиц (узлов) на каждом скрытом слое, поскольку мы не контролируем ни входной слой, ни размеры выходного слоя. Существует довольно много наборов функций активации, таких как Rectified Linear Unit, Sigmoid, Hyperbolic tangent и т. Д. . Исследования доказали, что более глубокие сети превосходят сети с большим количеством скрытых устройств.Поэтому всегда лучше и не повредит обучать более глубокую сеть (с уменьшающейся отдачей).
Давайте сначала представим некоторые обозначения, которые будут использоваться на протяжении всего сообщения:
Затем мы запишем размеры многослойной нейронной сети в общем виде, чтобы помочь нам в умножении матриц, поскольку одна из основных проблем в реализация нейронной сети позволяет получить правильные размеры.
Два уравнения, которые нам понадобятся для реализации прямого распространения, следующие: Эти вычисления будут выполняться на каждом уровне.
Сначала мы инициализируем матрицы весов и векторы смещения. Важно отметить, что мы не должны инициализировать все параметры равными нулю, потому что это приведет к тому, что градиенты будут равны, и на каждой итерации результат будет одинаковым, и алгоритм обучения ничего не узнает. Поэтому важно случайным образом инициализировать параметры значениями от 0 до 1. Также рекомендуется умножать случайные значения на небольшой скаляр, например 0,01, чтобы активировать блоки активации и находиться в областях, где производные функций активации не близки к нуль.{-z}) . Она превосходит сигмовидную функцию, в которой среднее значение ее выхода очень близко к нулю, что, другими словами, центрирует выход единиц активации вокруг нуля и делает диапазон значений очень маленьким, что означает более быстрое обучение. Недостаток, который он разделяет с сигмоидной функцией, заключается в том, что градиент очень мал на хорошей части домена.
Мы будем использовать двоичную стоимость Cross-Entropy . Он использует метод логарифма правдоподобия для оценки своей ошибки.Стоимость: указанная выше функция стоимости является выпуклой; однако нейронная сеть обычно застревает на локальном минимуме и не гарантирует, что найдет оптимальные параметры. Мы будем использовать здесь градиентное обучение.
Позволяет возвращаться информации от стоимости назад по сети для вычисления градиента. Следовательно, выполните цикл по узлам, начиная с последнего узла, в обратном топологическом порядке, чтобы вычислить производную выходных данных конечного узла по отношению к хвосту узла каждого ребра. Это поможет нам узнать, кто несет наибольшую ответственность за ошибку, и изменить параметры в этом направлении.i ∈ {0, 1} .
- Сначала загрузим изображения.
- Покажите образец изображения для кошки.
- Измените форму входной матрицы, чтобы каждый столбец был одним примером. Кроме того, поскольку каждое изображение имеет размер 64 x 64 x 3, у нас будет 12 288 функций для каждого изображения. Следовательно, матрица ввода будет 12 288 x 209.
- Стандартизируйте данные, чтобы градиенты не выходили из-под контроля. Кроме того, это поможет скрытым единицам иметь аналогичный диапазон значений. А пока мы разделим каждый пиксель на 255, что не должно быть проблемой.Однако лучше стандартизировать данные, чтобы получить среднее значение 0 и стандартное отклонение 1.
Исходные размеры:Рисунок 3: Образец изображения
--------------------
Обучение : (209, 64, 64, 3), (209,)
Тест: (50, 64, 64, 3), (50,) Новые размеры:
-------------- -
Обучение: (12288, 209), (1, 209)
Тест: (12288, 50), (1, 50)
Теперь наш набор данных готов для использования и тестирования нашего реализация нейронной сети. Давайте сначала напишем функцию многослойной модели для реализации обучения на основе градиента с использованием заранее определенного количества итераций и скорости обучения.
Далее мы обучим две версии нейронной сети, каждая из которых будет использовать разные функции активации на скрытых слоях: одна будет использовать выпрямленную линейную единицу ( ReLU ), а вторая будет использовать функцию гиперболического тангенса ( tanh ). ). Наконец, мы будем использовать параметры, полученные от обеих нейронных сетей, чтобы классифицировать обучающие примеры и вычислить уровни точности обучения для каждой версии, чтобы увидеть, какая функция активации лучше всего работает с этой задачей.
# Настройка яркости слоевРисунок 4: Кривая потерь с функцией активации tanh
Layers_dims = [X_train.shape [0], 5, 5, 1] # NN с активацией tanh fn
parameters_tanh = L_layer_model (X_train, y_train, Layers_dims, Learning_rate = 0.03, num_iterations = 3000, hidden_layers_activation_fn = "tanh") # Распечатать точность
precision (X_test , parameters_tanh, y_test, activate_fn = "tanh") Стоимость после 100 итераций: 0,6556
Стоимость после 200 итераций: 0,6468
Стоимость после 300 итераций: 0,6447
Стоимость после 400 итераций: 0,6441
Стоимость после 500 итераций это: 0.6440
Стоимость после 600 итераций: 0,6440
Стоимость после 700 итераций: 0,6440
Стоимость после 800 итераций: 0,6439
Стоимость после 900 итераций: 0,6439
Стоимость после 1000 итераций: 0,6439
Стоимость после 1100 итераций: 0,6439
Стоимость после 1200 итераций: 0,6439
Стоимость после 1300 итераций: 0,6438
Стоимость после 1400 итераций: 0,6438
Стоимость после 1500 итераций: 0,6437
Стоимость после 1600 итераций: 0 .6434
Стоимость после 1700 итераций: 0,6429
Стоимость после 1800 итераций: 0,6413
Стоимость после 1900 итераций: 0,6361
Стоимость после 2000 итераций: 0,6124
Стоимость после 2100 итераций: 0,5112
Стоимость после 2200 итераций: 0,5288
Стоимость после 2300 итераций: 0,4312
Стоимость после 2400 итераций: 0,3821
Стоимость после 2500 итераций: 0,3387
Стоимость после 2600 итераций: 0,2349
Стоимость после 2700 итераций: 0 .2206
Стоимость после 2800 итераций: 0,1927
Стоимость после 2900 итераций: 0,4669
Стоимость после 3000 итераций: 0,1040 «Уровень точности: 68,00%».
# NN с активацией relu fnРисунок 5: Кривая потерь с функцией активации ReLU
parameters_relu = L_layer_model (X_train, y_train, Layers_dims, Learning_rate = 0,03, num_iterations = 3000, hidden_layers_activation_fn = "relu "49) # Распечатать точность (X_test, parameters_relu, y_test, activate_fn = "relu") Стоимость после 100 итераций: 0.6556
Стоимость после 200 итераций: 0,6468
Стоимость после 300 итераций: 0,6447
Стоимость после 400 итераций: 0,6441
Стоимость после 500 итераций: 0,6440
Стоимость после 600 итераций: 0,6440
Стоимость после 700 итераций: 0,6440
Стоимость после 800 итераций: 0,6440
Стоимость после 900 итераций: 0,6440
Стоимость после 1000 итераций: 0,6440
Стоимость после 1100 итераций: 0,6439
Стоимость после 1200 итераций: 0 .6439
Стоимость после 1300 итераций: 0,6439
Стоимость после 1400 итераций: 0,6439
Стоимость после 1500 итераций: 0,6439
Стоимость после 1600 итераций: 0,6439
Стоимость после 1700 итераций: 0,6438
Стоимость после 1800 итераций: 0,6437
Стоимость после 1900 итераций: 0,6435
Стоимость после 2000 итераций: 0,6432
Стоимость после 2100 итераций: 0,6423
Стоимость после 2200 итераций: 0,6395
Стоимость после 2300 итераций: 0 .6259
Стоимость после 2400 итераций: 0,5408
Стоимость после 2500 итераций: 0,5262
Стоимость после 2600 итераций: 0,4727
Стоимость после 2700 итераций: 0,4386
Стоимость после 2800 итераций: 0,3493
Стоимость после 2900 итераций: 0,1877
Стоимость после 3000 итераций: 0,3641 «Уровень точности: 42,00%».
Обратите внимание, что приведенные выше показатели точности, как ожидается, будут завышать показатели точности обобщения.
Цель этого поста — пошагово написать код глубокой нейронной сети и объяснить при этом важные концепции. На данный момент нас особо не волнует уровень точности, так как есть множество вещей, которые мы могли бы сделать, чтобы повысить точность, о чем мы будем рассказывать в следующих публикациях. Ниже приведены некоторые выводы:
- Даже если нейронная сеть может представлять любую функцию, она может не обучаться по двум причинам:
- Алгоритм оптимизации может не найти наилучшее значение для параметров желаемой (истинной) функции. .Он может застрять в локальном оптимуме.
- Алгоритм обучения может найти другую функциональную форму, которая отличается от предполагаемой функции из-за переобучения.
- Даже если нейронная сеть редко сходится и всегда застревает в локальном минимуме, она все же может значительно снизить стоимость и создавать очень сложные модели с высокой точностью тестирования.
- Нейронная сеть, которую мы использовали в этом посте, представляет собой стандартную полностью подключенную сеть. Однако есть два других типа сетей:
- Сверточная сеть NN: где не все узлы подключены.Он лучший в своем классе для распознавания изображений.
- Recurrent NN: Есть соединения обратной связи, при которых выходные данные модели возвращаются в себя. Он используется в основном при последовательном моделировании.
- Полностью подключенная нейронная сеть также забывает, что произошло на предыдущих шагах, и ничего не знает о выходе.
- Существует ряд гиперпараметров, которые мы можем настроить с помощью перекрестной проверки, чтобы получить максимальную производительность нашей сети:
- Скорость обучения (α): Определяет, насколько велик шаг для каждого обновления параметров.
A. Малое α ведет к медленной сходимости и может стать очень дорогостоящим в вычислительном отношении.
B. Большое значение α может привести к перерегулированию, при котором наш алгоритм обучения может никогда не сходиться.
2. Количество скрытых слоев (глубина): чем больше скрытых слоев, тем лучше, но это требует больших вычислительных затрат.
3. Количество единиц на скрытый слой (ширина): исследования доказали, что огромное количество скрытых единиц на уровне не способствует улучшению сети.
4.Функция активации: какую функцию использовать на скрытых слоях, зависит от приложений и доменов. Это процесс проб и ошибок, чтобы попробовать разные функции и посмотреть, какая из них работает лучше всего.
5. Количество итераций.
- Стандартизация данных поможет активам иметь одинаковый диапазон значений и избежать выхода градиентов из-под контроля.
| Наименование компонента у производителя | БАЗА 8ВХ/8ВЫХ СВТД ПОЛЯРНОСТЬ 0/24В | |
| Группа продукции | Система быстрого монтажа Telefast 2 | |
| Activity | IDSAF | |
| COSL1 | EN | |
| 1 уровень иерархии | Программируемые логические контроллеры | |
| COSL2 | 0LX | |
| 2 уровень иерархии | Распределенный ввод/вывод для программируемых логических контроллеров, предназначенных для машин | |
| COSL3 | 2E5 | |
| 3 уровень иерархии | Ввод/вывод, Системы быстрого монтажа Telefast, As-i | |
| Минимальная партия к заказу | 1 | |
| Особенность заказа | ||
| Примечание | ||
| Страна происхождения | ||
| Сертификация RoHS | ||
| Код EAN / UPC | ||
| Код GPC | ||
| Код в Profsector.com | FS5.231.153.48 | |
| Статус компонента у производителя | C3(6) |
Аккумулятор FORSE 6СТ-60VLR (0) Обратная полярность 242*175*175
| Ёмкость | 60 Ач | |
| Пусковой ток | 640 А | |
| Габариты | 242x175x175 мм | |
| Полярность | обратная | |
| Страна производства | Россия |
FORSE (Форс) — легендарная торговая марка премиум-класса. По результатам независимых исследований рынка аккумуляторных батарей России в 2014, 2015, 2016 годах «Форс» емкостью 60 Ач вошли в тройку самых продаваемых АКБ. В 2016 году «Форс» 6СТ-60VL был назван аккумулятором года (на основе независимых тестов лаборатории ФГУП «НАМИ»)
Мощные аккумуляторы с повышенными пусковыми токами. Разработаны для иномарок и отечественных автомобилей с увеличенным количеством энергопотребителей на борту.
Конструктивные особенности:
— увеличенное количество электродов (в среднем на 20% больше чем в АКБ стандартной комплектации),
— положительный и отрицательный электроды выполнены из свинцово-кальциевого сплава,
— газоотводные каналы укомплектованы фильтрами-пламегасителями,
— диапазон рабочих температур: от -50 до +60 0С,
— гарантия 36 месяцев
Преимущества:
Высокий пусковой ток. Повышенный пусковой ток достигается путем использования большего количества электродов и применения специальных модифицированных углеродных и органических добавок для активной массы.
Устойчивость к глубоким разрядам. Данный показатель выделяет аккумуляторы марки «Форс» на фоне стандартных кальциевых батарей. Устойчивость к глубоким разрядам достигнута за счет применения специальных добавок, улучшающих прием заряда батареи в глубоко разряженном состоянии и способствующих восстановлению активной массы практически без потери электрических характеристик (при условии, что батарея была в глубоко разряженном состоянии не более 2-х дней).
Повышенная прочность электродов. Электроды повышенной прочности продлевают срок службы аккумуляторной батареи. Для повышения прочности электродов в активную массу вводятся полимерные армирующие материалы, а электродные пластины подвергаются обработке паром, в результате чего из свинецсодержащих материалов образуется устойчивый каркас, прочно соединенный химическими связями со свинцовой решеткой.
Минимальный расход воды. При нормальных условиях эксплуатации не требуется доливка воды на протяжении всего гарантийного срока службы батарей (достаточно заводского запаса). При перезаряде потеря воды минимальна.
Удобный. В отличие от импортных аналогов у аккумуляторов торговой марки «Форс» есть доступ к банкам, что значительно увеличивает срок службы аккумулятора. Доступ к банкам позволяет вовремя диагностировать состояние батареи и устранить проблему.
Учимся определять полярность автомобильного аккумулятора
Мне, человеку, связавшему свою пока еще короткую журналистскую карьеру с жизнеописаниями хитрых и своенравных аккумуляторных батарей, часто снится один и тот же кошмар.
Вот я прихожу в наш магазин «Автоша», вот выбираю батарейку нужной емкости, нужных габаритных размеров. Внимательно смотрю на параметры пускового тока – беру аккум с максимальными. Приезжаю домой, открываю капот своего авто и…
Даже не знаю, как описать этот ужас. Длины токоприемных проводов не хватает до клемм! В этот момент я понимаю, что НЕ ОБРАТИЛ ВНИМАНИЯ НА ПОЛЯРНОСТЬ аккумулятора! После такого осознания я немедленно просыпаюсь – прерывисто дыша и стирая со лба ледяной пот.
Эти кошмарные видения и натолкнули меня на мысль обезопасить вас, уважаемые читатели, от подобных катастроф в реальной жизни. Итак, какой же она может быть, эта коварная полярность.
Батареи для легковушек: реальные и условные виды полярности
Всего в аккумуляторной промышленности существует шесть типов компоновки и соединения между собой ячеек аккумуляторной батареи. Однако, большинство из них встречаются очень редко и рассматривать их под микроскопом мы не будем. Обратимся к самым распространенным и способам, как можно отличить их друг от друга.
Все типы полярности автомобильного аккумулятора
Перво-наперво, возьмемся за батарейки для легковых автомобилей. Берем аккумулятор и разворачиваем его к себе «лицом», то есть, этикеткой. Клеммы в этом случае будут находиться ближе к нам, на «макушке» нашего АКБ. Положительная (рядом с ней нарисован «+») находится справа, а минусовая(«-») слева? Перед вами аккумулятор с «обратной», по-другому – с «европейской» полярностью, которую часто обозначают «0».
Схема обратной полярности автомобильного аккумулятора
Если же положительный токовывод находится слева, а отрицательный – справа, то перед вами батарейка с полярностью «1» – «прямой» или «российской».
Схема прямой полярности автомобильного аккумулятора
Кстати, люди не сведущие зачастую говорят о некой «азиатской» полярности. На самом деле, речь идет об аккумуляторах, изготавливаемых для азиатских авто. Они имеют «европейскую» полярность, и отличаются только габаритами ( «квадратнее» коллег из Европы, США и России) и видом токовыводов. На обычных батареях клеммы слегка «утоплены» и находятся в нишах, а у «азиатских» они – на ровной поверхности. Кроме того, токовыводы «азиатов» заметно тоньше тех, что устанавливаются на батареях со всего мира.
Ну и, наконец, замолвим словечко еще об одном виде полярности легковых автомобилей – «американской полярности». Она встречается у батарей, предназначенных для автомобилей, произведенных на территории США. Клеммы у АКБ с «американской полярностью» находятся на фронтальной стороне, над лицевой этикеткой.
А как у грузовиков?
Клеммы на аккумуляторах для грузовых авто расположены по одной из коротких сторон батареи. Развернем АКБ этой самой стороной с клеммами к себе (можно мысленно, среди нас не все уродились гераклами). Слева «плюс» – полярность «3» – «европейская»/«обратная». Слева «минус» – значит полярность у батареи «4» – «прямая»/«российская».
Схема обратной полярности аккумулятора для грузового транспорта
Схема прямой полярности аккумулятора для грузового транспорта
Кроме того, могут встречаться грузовые аккумуляторы с полярностью “2” – клеммы у таких аккумуляторов расположены по диагонали.
Включаем Шерлока: что, если «плюс» не обозначен?
Конечно, производители стараются сделать аккумуляторы простыми и понятными для каждого пользователя. Положительные токовыводы отмечаются сразу бросающимися в глаза знаками «+» и красным цветом, отрицательные – не менее крупными «-» и синим/черным цветом. Но теоретически мы можем однажды оказаться наедине с батарейкой без всякой маркировки. Или с такой, маркировку которой уничтожили вредители, варвары, стихийные бедствия… Что делать тогда? Первым делом, мои пытливые друзья, необходимо измерить диаметр токовыводов. Диаметр положительных всегда на пару миллиметров больше диаметра отрицательных. У «европейцев» вывод плюсового электрода имеет толщину 19,5 миллиметров, а минусовая клемма – 17,9. У азиатов – 12,7 и 11,1 соответственно.
Данный метод определения плюсов-минусов тоже не дал результата? Что ж, теперь нам поможет только учебник занимательной химии для самых маленьких. К клеммам батареи без опознавательных знаков необходимо прикрепить медные проводки. Оголенные концы проводков вводим в картофельный срез на расстоянии 5-10 мм друг от друга. Ждем 1-2 минуты. Эврика! Картофель вокруг «положительного» проводка слегка позеленеет.
Под рукой нет картошки, но есть, к примеру, лимонная или любая другая слабая кислота? Пожалуйста! Разводим ее в стакане воды, погружаем в него проводки от обеих клемм так, чтобы они не соприкасались. Вокруг «отрицательного» проводка начнется бурное выделение пузырьков газа.
Теперь, уважаемые читатели, когда вы знаете о «минусах» и «плюсах» аккумуляторов практически все, кошмары меня, надеюсь, оставят. А за вас – никогда не возьмутся, ни во сне, ни наяву!
Аккумуляторная батарея PREMIUM [12V 53Ah 540A B13]207x175x190mm,Полярность ETN 0 [-/+],Тип клеммы 1(EN) [«+» d 19.5,»-» d17.9] EXIDE EA530
- Главная /
- Бренды /
- Exide /
- Exide EA530 Аккумуляторная батарея PREMIUM [12V 53Ah 540A B13]207x175x190mm,Полярность ETN 0 [-/+],Тип клеммы 1(EN) [«+» d 19.5,»-» d17.9]
| Полярность | 0 |
| Производитель | EXIDE |
| Размеры (Д/Ш/В) | 207x175x190 |
| Пусковой ток | 540 |
| Емкость | 53 |
Информация для покупателей
ВНИМАНИЕ! Обязательно ношение масок! Минимальная сумма заказа для соблюдения срока поставки 24 часа и заказ 3 часа 1000руб Аналоги и замены на сайте используются только в виде справочной информации! Просьба перепроверять их с помощью оригинальных программ. При самостоятельном подборе детали Вы несете ответственность за ее применяемость к вашему автомобилю.
Информация для покупателей
Минимальная сумма заказа для соблюдения срока поставки 24 часа и заказ 3 часа 1000руб
Почему EXIDE EA530 с номером EA530 фирмы EXIDE покупают в магазине Автозапчасти52.рф :
- Только надежные поставщики
Наш магазин запчастей является поставщиком EXIDE (артикул EA530) на территории Нижнего Новгорода и региона, поэтому у нас лучшие цена на Аккумуляторная батарея PREMIUM [12V 53Ah 540A B13]207x175x190mm,Полярность ETN 0 [-/+],Тип клеммы 1(EN) [«+» d 19.5,»-» d17.9] производства EXIDE.
- Гарантия качества
На все запчасти бренда EXIDE предоставляется гаратния.
- Важно перед заказом знать
Каждый номер EA530 имеет свою применимость, поэтому перед заказом убедитесь что данная деталь Аккумуляторная батарея PREMIUM [12V 53Ah 540A B13]207x175x190mm,Полярность ETN 0 [-/+],Тип клеммы 1(EN) [«+» d 19.5,»-» d17.9] подходит на Ваш автомобиль.
- Удобный on-line сервис
Так же можете купить аналоги EXIDE (артикул EA530) или позвоните нам, и мы вам поможем. Телефон: +7 (831) 291-58-99
Срок доставки указан в рабочих днях, и рассчитывается со следующего дня после оплаты заказа до прихода детали в выбранный филиал
Пожалуйста, учитывайте возможные изменения сроков доставки при планировании ремонтных работ.
- Цена на EXIDE (артикул EA530)
Отличная стоимость товара достигается исходя из прямых поставок со складов дистрьеютеров данного бренда EXIDE.
Обращаем внимание, указание ТОВАРНЫХ ЗНАКОВ (наименований марок автомобилей) направлено на информирование покупателей о применимости запасной части к той или иной марке автомобиля, то есть на потребительские свойства товара. Данная информация не вводит потребителя в заблуждение относительно предлагаемых к продаже запасных частей для автомобилей и его производителей, не нарушает права правообладателей указанных товарных знаков. Требование предоставлять покупателю необходимую и достоверную информацию о товаре, предлагаемом к продаже, обеспечивающую возможность их правильного выбора возложено на продавца (изготовителя) Законом «О защите прав потребителей», ст. 495 ГК РФ.
Полярность аккумулятора — что означает и как правильно определить полярность?
Полярность – расположение на крышке аккумулятора присоединительных клемм, которые являются токовыводящими элементами. Так как полюса всего два – положительный и отрицательный, то и вариантов расположения их немного – прямое и обратное. Мы рассмотрим по отношению к чему принято определять расположение клемм, что будет если случайно перепутать полюса, когда специально делается переполюсовка.
Что означает прямая и обратная полярность аккумулятора
Расположение клемм на аккумуляторе происходит всегда в определенной последовательности, по стандарту стран производителей. Клеммы всего две, плюс и минус. Они могут иметь разное положение, но наиболее удобным для обслуживания оказалось вынести клеммы на крышку. При этом они бывают поднятыми или утопленными, отличая европейский и азиатский тип.
Клеммы удобно располагать на крышке с двух сторон. Прямая и обратная полярность отличают аккумуляторы только переменой места полюсов. Если прямым считают положение, когда ты читаешь надписи на лицевой стороне, а правая рука касается правой плюсовой кнопки. Обратное положение- та же рука касается отрицательной кнопки.
Это важно учитывать, покупая аккумулятор взамен старого. Подключать клеммы наоборот будет неудобно, придется наращивать один провод, укорачивать другой.
Как определить – полярность аккумулятора прямая или обратная
У каждого аккумулятора есть лицевая сторона, снабженная маркетинговыми и информационными наклейками. Если поставить аккумулятор лицом к себе, клеммы располагаются по правую и левую руку.
«Прямая» полярность в маркировке иногда отмечается цифрой 1. Это российская компоновка аккумуляторов. Если аккумулятор стоит лицом, плюсовая кнопка под левой рукой, красная или с рифленым плюсом. Правая — отрицательная
«Обратная» полярность в классификациях отмечается цифрой «0». Чтобы определиться, нужно поставить аккумулятор лицом к себе. Левая рука ляжет на отрицательную клемму, а правая – на положительную.
Прямая и обратная полярность обозначают различие во внутренней схеме контактов банок на ту или другую сторону. Практически это значит, при замене аккумулятора владелец может перепутать полюса при подключении к шинам авто.
Разница между прямой и обратной полярностью аккумулятора
Ничем другим, кроме расположения полюсов, прямые и обратные схемы соединения банок в батарею не отличаются. Но при установке в гнездо не того аккумулятора могут возникнуть проблемы. Их будет еще больше, если не подойдут провода или перепутаете полярность.
Полярность грузовых аккумуляторов
Конечно, лучше поставить аккумулятор правильной полярности, но места под капотом больше, провода длиннее, поэтому правильно подсоединить можно любой аккумулятор. Важно не перепутать полюса при сборке схемы. В связи с тем что аккумуляторы для грузовиков габаритнее, вариантов подсоединения в них больше — полюса располагаются по вертикали, горизонтали и диагонали, меняясь местами.
Как определить полярность аккумулятора
На грузовых авто установлены емкие и тяжелые аккумуляторы. У них точно также как определяется прямая и обратная полярность. Справа положительный полюс – прямая полярность, отрицательный – обратная. Только смотреть нужно не с лица, а со стороны, где ближе выводы. И обратная полярность в грузовом авто маркируется цифрой «3», а прямая цифрой «4». Если контакты расположились по диагонали – они маркируются цифрой «2». Есть еще виды расположения полюсов с маркировкой «9» и «6»
Что означает обратная полярность аккумулятора
Обратная полярность значит предусмотрена вариативность посадки – относительное расположение полюсов аккумуляторов даже у одного производителя может быть прямым и обратным. Это позволяет эффективнее использовать подкапотное пространство, делая удобную компоновку. Тем важнее выбрать точно такой же аккумулятор. Если полярность обратная, независимо, в грузовой или легковой машине, катод будет всегда находиться под правой рукой, при условии, что аккумулятор стоит правильно.
Смена полярности аккумулятора
Смена полярности аккумулятора может произойти случайно или преднамеренно. Если вы перепутали клеммы при прикуривании – материальные издержки как донору, так и акцептору обеспечены.
Если случайно произвели смену полярности в своем авто, то в лучшем случае сгорит главный предохранитель, в худшем – диодный мост. Чем быстрее заметили косяк – тем меньше потери.
Смена полярности, как переполюсовка применяется для возвращения работоспособности сульфатированному АКБ. Аккумулятор с аппетитом ест сульфат свинца, очищая пластины. Но переполюсовка – работа аккумулятора вопреки правилам. Вынужденная мера должна быть временной. Гораздо лучше использовать при десульфатации двойную смену полярности.
Видео
Полярность прямая, обратная – вроде бы ясно все. Но случаются эксцессы. Предлагаем видео по теме.
3.5.0: Электроотрицательность и полярность — Chemistry LibreTexts
Электроотрицательность и тип связи
Абсолютное значение разницы в электроотрицательности (ΔEN) двух связанных атомов дает приблизительную меру ожидаемой полярности в связи и, следовательно, типа связи. Когда разница очень мала или равна нулю, связь ковалентная и неполярная. Когда он большой, связь полярная ковалентная или ионная. Абсолютные значения разности электроотрицательностей между атомами в связях H – H, H – Cl и Na – Cl равны 0 (неполярный), 0.9 (полярный ковалентный) и 2.1 (ионный) соответственно. Степень, в которой электроны распределяются между атомами, варьируется от полностью равной (чистая ковалентная связь) до нулевой (ионная связь). На рисунке \ (\ PageIndex {2} \) показана взаимосвязь между разностью электроотрицательностей и типом связи.
Рисунок \ (\ PageIndex {2} \): По мере увеличения разницы электроотрицательностей между двумя атомами связь становится более ионной.
Грубое приближение различий электроотрицательности, связанных с ковалентными, полярными ковалентными и ионными связями, показано на рисунке \ (\ PageIndex {4} \).Однако эта таблица является лишь общим руководством, за множеством исключений. Например, атомы H и F в HF имеют разность электроотрицательностей 1,9, а атомы N и H в NH 3 разность 0,9, однако оба этих соединения образуют связи, которые считаются полярными ковалентными. Аналогично, атомы Na и Cl в NaCl имеют разность электроотрицательностей 2,1, а атомы Mn и I в MnI 2 имеют разность 1,0, но оба эти вещества образуют ионные соединения.
Лучшим руководством к ковалентному или ионному характеру связи является рассмотрение типов задействованных атомов и их относительного положения в периодической таблице.Связи между двумя неметаллами обычно ковалентны; связь между металлом и неметаллом часто ионная.
Некоторые соединения содержат как ковалентные, так и ионные связи. Атомы в многоатомных ионах, таких как OH — , \ (\ ce {NO3 -} \) и \ (\ ce {Nh5 +} \), удерживаются вместе полярными ковалентными связями. Однако эти многоатомные ионы образуют ионные соединения, соединяясь с ионами противоположного заряда. Например, нитрат калия, KNO 3 , содержит катион K + и многоатомный анион \ (\ ce {NO3 -} \).Таким образом, связь в нитрате калия является ионной, что является результатом электростатического притяжения между ионами K + и \ (\ ce {NO3 -} \), а также ковалентности между атомами азота и кислорода в \ (\ ce {NO3 -} \).
Пример \ (\ PageIndex {1} \): электроотрицательность и полярность связи
Полярность связей играет важную роль в определении структуры белков. Используя значения электроотрицательности в таблице A2, расположите следующие ковалентные связи — все обычно присутствующие в аминокислотах — в порядке увеличения полярности.Затем обозначьте положительный и отрицательный атомы символами δ + и δ–:
C – H, C – N, C – O, N – H, O – H, S – H
Решение
Полярность этих связей увеличивается с увеличением абсолютного значения разности электроотрицательностей. Атом с обозначением δ– является более электроотрицательным из двух. Таблица \ (\ PageIndex {1} \) показывает эти связи в порядке возрастания полярности.
| Облигация | ΔEN | Полярность |
|---|---|---|
| C – H | 0.4 | \ (\ overset {δ -} {\ ce C} — \ overset {δ +} {\ ce H} \) |
| S – H | 0,4 | \ (\ overset {δ -} {\ ce S} — \ overset {δ +} {\ ce H} \) |
| C – N | 0,5 | \ (\ overset {δ +} {\ ce C} — \ overset {δ -} {\ ce N} \) |
| N – H | 0,9 | \ (\ overset {δ -} {\ ce N} — \ overset {δ +} {\ ce H} \) |
| C – O | 1.0 | \ (\ overset {δ +} {\ ce C} — \ overset {δ -} {\ ce O} \) |
| O – H | 1,4 | \ (\ overset {δ -} {\ ce O} — \ overset {δ +} {\ ce H} \) |
Полярность связи | Химия для неосновных
Цели обучения
- Определите электроотрицательность.
- Используйте значения электроотрицательности для определения типа связи.
Вы когда-нибудь проводили время с тем, кто вам действительно не нравился? Вы не имели с ними ничего общего и не хотели иметь с ними ничего общего.С другой стороны, есть люди, с которыми вам нравится быть. У вас много общего, и вы любите с ними делиться. Атомы работают точно так же. Если есть сильные различия в их притяжении электронов, один атом получает электроны, а другой атом теряет их. Если они похожи, они разделяют электроны, образуя ковалентную связь.
Электроотрицательность определяется как способность атома притягивать электроны, когда атомы находятся в соединении. Электроотрицательность элементов показана в таблице Менделеева ниже.
Рисунок 1. Электроотрицательность элементов.
Рис. 2. Тип связи основан на разнице в электроотрицательности двух элементов, участвующих в связи.
Степень, в которой данная связь является ионной или ковалентной, определяется путем вычисления разницы в электроотрицательности между двумя атомами, участвующими в связи.
В качестве примера рассмотрим связь, которая возникает между атомом калия и атомом фтора. По таблице разница электроотрицательностей равна 4.0 — 0,8 = 3,2.
Поскольку разница в электроотрицательности относительно велика, связь между двумя атомами является ионной. Поскольку атом фтора имеет гораздо большее притяжение электронов, чем атом калия, валентный электрон от атома калия полностью передается атому фтора. На приведенной ниже диаграмме показано, как разница в электроотрицательности связана с ионным или ковалентным характером химической связи.
Неполярные ковалентные связи
Связь, в которой разница электроотрицательностей меньше 1.7 считается в основном ковалентным по своему характеру. Однако на этом этапе нам нужно различать два общих типа ковалентных связей.
Неполярная ковалентная связь представляет собой ковалентную связь, в которой связывающие электроны распределяются поровну между двумя атомами. В неполярной ковалентной связи распределение электрического заряда между двумя атомами сбалансировано.
Рис. 3. Неполярная ковалентная связь — это связь, в которой распределение электронной плотности между двумя атомами одинаково.
Два атома хлора в равной степени разделяют пару электронов в одинарной ковалентной связи, а электронная плотность, окружающая молекулу Cl 2 , является симметричной. Также обратите внимание, что молекулы, в которых разница электроотрицательностей очень мала (<0,4), также считаются неполярными ковалентными. Примером может служить связь между хлором и бромом.
Полярные ковалентные связи
Рис. 4. В полярной ковалентной связи HF электронная плотность распределена неравномерно.У атома фтора более высокая плотность (красный), а у атома водорода — более низкая (синий).
Связь, в которой разница электроотрицательностей между атомами составляет от 0,4 до 1,7, называется полярной ковалентной связью.
Полярная ковалентная связь — это ковалентная связь, в которой атомы имеют неодинаковое притяжение для электронов, и поэтому их совместное использование неодинаково. В полярной ковалентной связи, которую иногда называют просто полярной связью, распределение электронов вокруг молекулы больше не симметрично.
Простой способ проиллюстрировать неравномерное распределение электронов в полярной ковалентной связи — использовать греческую букву дельта ( δ ).
Рис. 5. Использование δ для обозначения частичного заряда.
Атом с большей электроотрицательностью приобретает частичный отрицательный заряд, а атом с меньшей электроотрицательностью приобретает частичный положительный заряд. Символ дельты используется, чтобы указать, что количество заряда меньше единицы. Перекрещенная стрелка также может использоваться для обозначения направления большей электронной плотности.
Рисунок 6. Перекрещенная стрелка указывает полярность.
Резюме
- Электроотрицательность атома определяет, насколько сильно он притягивает к себе электроны.
- На полярность связи влияют значения электроотрицательности двух атомов, входящих в эту связь.
Практика
Пройдите тест в правой части страницы:
http://www.sophia.org/determining-bond-polarity/determining-bond-polarity-tutorial
Обзор
- Тип облигации с разницей в 1.9?
- Какой будет тип облигации для BH 2 ?
- Ваш друг говорит вам, что связь LiF ковалентна. Что ты говоришь?
Глоссарий
- электроотрицательность: Способность атома притягивать электроны, когда атомы находятся в составе.
- неполярная ковалентная связь: Ковалентная связь, в которой связывающие электроны распределяются поровну между двумя атомами.
- полярная ковалентная связь: Ковалентная связь, в которой атомы обладают неодинаковым притяжением для электронов, и поэтому их совместное использование неодинаково.
Форма молекулы и полярность | Безграничная химия
Дипольный момент
Диполь существует, когда молекула имеет области асимметричного положительного и отрицательного заряда.
Цели обучения
Предскажите, какие молекулы будут иметь низкий и высокий дипольный момент.
Основные выводы
Ключевые моменты
- Диполь существует, когда молекула имеет области асимметричного положительного и отрицательного заряда.
- Полярность молекулы (ее диполь) может быть определена экспериментально путем измерения диэлектрической проницаемости.
- Геометрия молекул имеет решающее значение при работе с диполями.
Ключевые термины
- диполь : любая молекула или радикал, имеющий делокализованный положительный и отрицательный заряды
- debye : единица СГС электрического дипольного момента, эквивалентная 3,33564 x 10-30 кулонов метров; используется для измерений в молекулярном масштабе
Диполь существует, когда в молекуле есть области асимметричных положительных и отрицательных зарядов.Дипольные моменты увеличиваются с характером ионной связи и уменьшаются с характером ковалентной связи.
Дипольный момент связи
Дипольный момент связи использует идею электрического дипольного момента для измерения полярности химической связи внутри молекулы. Это происходит всякий раз, когда есть разделение положительных и отрицательных зарядов из-за неравного притяжения, которое два атома имеют к связанным электронам. Атом с большей электроотрицательностью будет иметь большее притяжение для связанных электронов, чем атом с меньшей электроотрицательностью; чем больше разница в двух электроотрицательностях, тем больше диполь.Так обстоит дело с полярными соединениями, такими как фтористый водород (HF), где атомы имеют неодинаковую электронную плотность.
Физик-химик Питер Дж. У. Дебай был первым, кто всесторонне изучил молекулярные диполи. Дипольные моменты связи обычно измеряются в дебайах, представленных символом D.
Молекулы с двумя атомами содержат только одну (одинарную или кратную) связь, поэтому дипольный момент связи — это дипольный момент молекулы. Их значения варьируются от 0 до 11 D. С одной стороны, симметричная молекула, такая как хлор, Cl 2 , имеет дипольный момент 0.Это тот случай, когда электроотрицательность обоих атомов одинакова. С другой стороны, высокоионный бромид калия в газовой фазе, KBr, имеет дипольный момент 10,5 D.
Симметрия Бонда
Симметрия — еще один фактор, определяющий, имеет ли молекула дипольный момент. Например, молекула диоксида углерода имеет две связи углерод-кислород, полярные из-за разницы электроотрицательностей между атомами углерода и кислорода. Однако связи находятся как раз на противоположных сторонах от центрального атома, заряды компенсируются.В результате углекислый газ — неполярная молекула.
Линейная структура диоксида углерода. : Две связи углерода с кислородом полярны, но они находятся на расстоянии 180 ° друг от друга и аннулируются.
Молекулярный дипольный момент
Когда молекула состоит из более чем двух атомов, более чем одна связь удерживает молекулу вместе. Чтобы вычислить диполь для всей молекулы, добавьте все отдельные диполи отдельных связей в качестве их вектора. Значения дипольного момента могут быть получены экспериментально путем измерения диэлектрической проницаемости.Некоторые типичные значения газовой фазы в единицах дебая включают:
- углекислый газ: 0 (несмотря на наличие двух полярных связей C = O, они направлены в геометрически противоположные направления, компенсируя друг друга и приводя к молекуле без суммарного дипольного момента)
- окись углерода: 0,112 D
- озон: 0,53 D
- фосген: 1,17 D
- водяной пар: 1,85 D
- цианистый водород: 2,98 D
- цианамид: 4,27 D
- калия бромид: 10.41 D
KBr имеет один из самых высоких дипольных моментов из-за значительной разницы в электроотрицательности между калием и бромом.
Полярность связи
Полярность связи существует, когда два связанных атома неодинаково разделяют электроны, что приводит к отрицательному и положительному концу.
Цели обучения
Определите факторы, определяющие полярность химической связи.
Основные выводы
Ключевые моменты
- Неравное распределение электронов внутри связи приводит к образованию электрического диполя (разделению положительных и отрицательных электрических зарядов).
- Чтобы определить распределение электронов между двумя атомами, таблица электроотрицательностей может определить, какой атом будет привлекать больше электронной плотности.
- Связи могут находиться между одной из двух крайностей: от полностью неполярной до полностью полярной.
Ключевые термины
- электроотрицательность : склонность атома или молекулы притягивать электроны и, таким образом, образовывать связи
- связь : связь или сила между соседними атомами в молекуле
В химии полярность связи — это разделение электрического заряда вдоль связи, приводящее к тому, что молекула или ее химические группы обладают электрическим дипольным или дипольным моментом.
Электроны не всегда распределяются поровну между двумя связующими атомами. Один атом может оказывать на электронное облако большую силу, чем другой; это притяжение называется электроотрицательностью. Электроотрицательность измеряет притяжение конкретного атома для электронов. Неравное распределение электронов внутри связи приводит к образованию электрического диполя (разделению положительного и отрицательного электрического заряда). Частичные заряды обозначаются как δ + (дельта плюс) и δ- (дельта минус), символы, которые были введены Кристофером Ингольдом и его женой Хильдой Ашервуд в 1926 году.
Атомы с высокими значениями электроотрицательности, такие как фтор, кислород и азот, сильнее притягивают электроны, чем атомы с более низкими значениями электроотрицательности. В связи это может привести к неравному распределению электронов между атомами, поскольку электроны будут притягиваться ближе к атому с более высокой электроотрицательностью.
Полярная ковалентная связь, HF. : более электроотрицательный (4,0> 2,1) фтор притягивает электроны в связи ближе к себе, образуя частичный отрицательный заряд.Образующийся атом водорода несет частичный положительный заряд.
Связи могут находиться между одной из двух крайностей: от полностью неполярной до полностью полярной. Полностью неполярная связь возникает, когда значения электроотрицательности идентичны и, следовательно, имеют нулевую разницу. Полностью полярная связь, или ионная связь, возникает, когда разница между значениями электроотрицательности настолько велика, что один атом фактически забирает электрон у другого. Термины «полярный» и «неполярный» обычно относятся к ковалентным связям.Чтобы определить полярность ковалентной связи с помощью числовых средств, найдите разницу между электроотрицательностью атомов; если результат составляет от 0,4 до 1,7, то, как правило, связь полярно-ковалентная.
Молекула фтороводорода (HF) полярна благодаря полярным ковалентным связям; в ковалентной связи электроны смещаются к более электроотрицательному атому фтора.
Процентный ионный характер и угол связи
Химические связи более разнообразны, чем можно предположить по терминологии; они существуют в спектре чисто ионных и чисто ковалентных связей.
Цели обучения
Признайте разницу между теоретическими и наблюдаемыми свойствами ионных связей.
Основные выводы
Ключевые моменты
- Спектр связи (ионной и ковалентной) зависит от того, насколько равномерно электроны распределяются между двумя атомами.
- Ионный характер связи — это количество электронов, которыми совместно пользуются два атома; ограниченное совместное использование электронов соответствует высокому процентному ионному характеру.
- Чтобы определить процентный ионный характер связи, электроотрицательность атомов используется для прогнозирования распределения электронов между атомами.
Ключевые термины
- ковалентная связь : два атома связаны друг с другом за счет совместного использования двух или более электронов
- ионная связь : два атома или молекулы связаны друг с другом электростатическим притяжением
Ионные связи в реальности
Когда два элемента образуют ионное соединение, действительно ли электрон теряется одним атомом и передается другому? Чтобы ответить на этот вопрос, рассмотрим данные о твердом ионном LiF.Средний радиус нейтрального атома Li составляет около 2,52 Å. Если этот атом Li реагирует с атомом F с образованием LiF, каково среднее расстояние между ядром Li и электроном, который он «потерял» из-за атома фтора? Ответ 1,56 Å; электрон теперь ближе к ядру лития, чем был в нейтральном литии.
Связывание во фториде лития : Где находится электрон во фториде лития? Создает ли это ионную связь, ковалентную связь или что-то среднее?
Ответ на вышеупомянутый вопрос — и да, и нет: да, электрон, который сейчас находился на 2s-орбитали Li, теперь находится в пределах досягаемости фторсодержащей 2p-орбитали; но нет, электрон теперь даже ближе к ядру Li, чем раньше, так что он на самом деле не «потерян».”
Связь электронных пар явно ответственна за эту ситуацию; это обеспечивает стабильность ковалентной связи. Что не так очевидно — пока вы не посмотрите на числа, подобные приведенным выше для LiF, — это то, что ионная связь приводит к тому же состоянию; даже в самых высокоионных соединениях оба электрона находятся рядом с обоими ядрами, и возникающие в результате взаимные притяжения связывают ядра вместе.
Возникающий взгляд на ионную связь — это такая, в которой электронные орбитали соседних пар атомов просто перекошены, создавая большую электронную плотность вокруг «отрицательного» элемента, чем вокруг «положительного».Думайте о величине этого перекоса как о процентном ионном характере связи; чтобы определить процентный ионный характер, нужно посмотреть на электроотрицательность задействованных атомов и определить, насколько эффективно обмен электронами между частицами.
Однако модель ионной связи полезна для многих целей. Нет ничего плохого в использовании термина «ионная связь» для описания взаимодействий между атомами в очень небольшом классе «ионных твердых тел», таких как LiF и NaCl.
Угол крепления
Валентный угол образуется между тремя атомами по крайней мере через две связи.Чем более ковалентна по природе связь, тем более вероятно, что атомы будут располагаться вдоль заранее определенных векторов, заданных орбиталями, которые участвуют в связывании (теория VSEPR). Чем больше ионный характер связи, тем более вероятно, что ненаправленные электростатические взаимодействия удерживают атомы вместе. Это означает, что атомы будут располагаться в положениях, которые минимизируют занимаемое ими пространство (например, кристалл соли).
Quickstart — документация TextBlob 0.16.0
TextBlob предоставляет доступ к обычным операциям обработки текста через знакомый интерфейс.Вы можете обрабатывать объекты TextBlob , как если бы они были строками Python, которые научились выполнять обработку естественного языка.
Создание TextBlob
Во-первых, импорт.
>>> из импорта текстовых блоков TextBlob
Давайте создадим наш первый TextBlob .
>>> wiki = TextBlob («Python - это язык программирования общего назначения высокого уровня.»)
Маркировка части речи
Теги части речи доступны через свойство tags .
>>> wiki.tags
[('Python', 'NNP'), ('is', 'VBZ'), ('a', 'DT'), ('high-level', 'JJ'), ('универсальный', 'JJ'), ('программирование', 'NN'), ('язык', 'NN')]
Анализ настроений
Свойство тональность возвращает именованный кортеж в форме Настроение (полярность, субъективность) . Оценка полярности является плавающей в диапазоне [-1,0, 1,0]. Субъективность — это плавающее значение в диапазоне [0,0, 1,0], где 0,0 — очень объективный, а 1,0 — очень субъективный.
>>> testimonial = TextBlob ("Textblob удивительно прост в использовании. Какое веселье!")
>>> testimonial.sentiment
Настроение (полярность = 0,39166666666666666, субъективность = 0,4357142857142857)
>>> testimonial.sentiment.polarity
0,39166666666666666
Токенизация
Вы можете разбить текстовые блоки на слова или предложения.
>>> zen = TextBlob («Красивое лучше уродливого». ... "Явное лучше, чем неявное." ... «Лучше простое, чем сложное».) >>> zen.words WordList (['Красиво', 'есть', 'лучше', 'чем', 'уродливо', 'Явно', 'есть', 'лучше', 'чем', 'неявно', 'Простое', 'есть' , 'лучше', 'чем', 'сложный']) >>> zen.sentences [Предложение («Красивое лучше, чем уродство.»), Предложение («Явное лучше, чем неявное.»), Предложение («Простое лучше, чем сложное».)]
Объекты Sentence имеют те же свойства и методы, что и TextBlobs.
>>> для предложения в дзен.предложения: ... печать (предложение. суждение)
Для более продвинутой токенизации см. Руководство по расширенному использованию.
Флексия и лемматизация слов
Каждое слово в TextBlob.words или Sentence.words — это Word объект (подкласс unicode ) с полезными методами, например для словоизменения.
>>> предложение = TextBlob ('Используйте 4 пробела на уровень отступа.')
>>> предложение.слова
WordList (['Использовать', '4', 'пробелы', 'за', 'отступ', 'уровень'])
>>> предложение.слова [2] .singularize ()
'пространство'
>>> предложение.words [-1] .pluralize ()
"уровни"
Слова можно лемматизировать, вызвав метод лемматизации .
>>> из текстовых блоков импорта Word
>>> w = Слово ("осьминоги")
>>> w.lemmatize ()
'осьминог'
>>> w = Word ("пошел")
>>> w.lemmatize ("v") # Передать в WordNet часть речи (глагол)
'идти'
Интеграция WordNet
Вы можете получить доступ к synset’ам для Word через свойство synsets или метод get_synsets , при необходимости передавая часть речи.
>>> из текстовых блоков импорта Word
>>> из textblob.wordnet импортировать ГЛАГОЛ
>>> word = Word ("осьминог")
>>> word.synsets
[Synset ('octopus.n.01'), Synset ('octopus.n.02')]
>>> Word ("взломать"). Get_synsets (pos = VERB)
[Synset ('chop.v.05'), Synset ('hack.v.02'), Synset ('hack.v.03'), Synset ('hack.v.04'), Synset ('hack. v.05 '), Synset (' hack.v.06 '), Synset (' hack.v.07 '), Synset (' hack.v.08 ')]
Вы можете получить доступ к определениям для каждого набора synset с помощью свойства definitions или метода define () , который также может принимать необязательный аргумент части речи.
>>> Слово («осьминог»). Определения [«щупальца осьминога, приготовленные в пищу», «головоногие моллюски, живущие на дне, имеющие мягкое овальное тело с восемью длинными щупальцами»]
Вы также можете создавать синсеты напрямую.
>>> из textblob.wordnet import Synset
>>> осьминог = Synset ('octopus.n.02')
>>> креветка = Synset ('shrimp.n.03')
>>> octopus.path_similarity (креветка)
0,1111111111111111
Дополнительные сведения об API WordNet см. В документации NLTK по интерфейсу Wordnet.
Списки слов
A WordList — это просто список Python с дополнительными методами.
>>> animals = TextBlob («кошка, собака, осьминог») >>> животные. слова WordList (['кошка', 'собака', 'осьминог]) >>> animals.words.pluralize () WordList (['кошки', 'собаки', 'осьминоги'])
Исправление орфографии
Используйте метод правильно () , чтобы попытаться исправить орфографию.
>>> b = TextBlob ("У меня хорошее правописание!")
>>> print (б.верный())
У меня хорошее правописание!
Объекты Word имеют метод spellcheck () Word.spellcheck () , который возвращает список из (слово, достоверность) кортежей с вариантами правописания.
>>> из текстовых блоков импорта Word
>>> w = Слово ('ошибочность')
>>> w.spellcheck ()
[('подверженность ошибкам', 1.0)]
Коррекция орфографии основана на книге Питера Норвига «Как написать корректор орфографии», реализованной в библиотеке шаблонов.Это около 70% точности.
Получение частотных словосочетаний и словосочетаний
Есть два способа узнать частоту слова или существительной фразы в TextBlob .
Первый — через словарь word_counts .
>>> monty = TextBlob ("Мы больше не Рыцари, которые говорят Ни."
... «Теперь мы Рыцари, которые говорят: Ekki ekki ekki PTANG.»)
>>> monty.word_counts ['ekki']
3
Если вы получите доступ к частотам таким образом, поиск будет , а не с учетом регистра, и слова, которые не найдены, будут иметь частоту 0.
Второй способ — использовать метод count () .
>>> monty.words.count ('ekki')
3
Вы можете указать, должен ли поиск выполняться с учетом регистра (по умолчанию Ложь ).
>>> monty.words.count ('ekki', case_sensitive = True)
2
Каждый из этих методов также можно использовать с именными фразами.
>>> wiki.noun_phrases.count ('питон')
1
Разбор
Используйте метод parse () для анализа текста.
>>> b = TextBlob ("А теперь о другом.")
>>> print (b.parse ())
И / CC / O / O сейчас / RB / B-ADVP / O для / IN / B-PP / B-PNP что-то / NN / B-NP / I-PNP полностью / RB / B-ADJP / O другое / JJ / I-ADJP / O ././O/O
По умолчанию TextBlob использует синтаксический анализатор шаблона.
TextBlobs похожи на строки Python!
Вы можете использовать синтаксис подстроки Python.
>>> дзен [0:19] TextBlob («Красивое лучше»)
Вы можете использовать обычные строковые методы.
>>> zen.upper ()
TextBlob («КРАСИВОЕ ЛУЧШЕ, ЧЕМ УЖЕ. ЯВНОЕ ЛУЧШЕ, ЧЕМ НЕЯВНОЕ. ПРОСТОЕ ЛУЧШЕ, ЧЕМ СЛОЖНОЕ.»)
>>> zen.find ("Простой")
65
Вы можете сравнивать TextBlobs и строки.
>>> apple_blob = TextBlob ('яблоки')
>>> banana_blob = TextBlob ('бананы')
>>> apple_blob <банановый_blob
Истинный
>>> apple_blob == 'яблоки'
Истинный
Вы можете объединять и интерполировать TextBlobs и строки.
>>> apple_blob + 'и' + banana_blob
TextBlob («яблоки и бананы»)
>>> "{0} и {1}". Формат (apple_blob, banana_blob)
'яблоки и бананы'
n -грамм Метод TextBlob.ngrams () возвращает список кортежей из n последовательных слов.
>>> blob = TextBlob («Лучше сейчас, чем никогда»). >>> blob.ngrams (n = 3) [WordList (['Сейчас', 'есть', 'лучше']), WordList (['есть', 'лучше', 'чем']), WordList (['лучше', 'чем', 'никогда'] )]
Получить индексы начала и окончания предложений
Используйте предложений.начало и предложение. конец , чтобы получить индексы, в которых предложение начинается и заканчивается в TextBlob .
>>> для s в дзен. Предложениях:
... печать (и)
... print ("---- Начинается с индекса {}, заканчивается с индекса {}". format (s.start, s.end))
Красивое лучше уродливого.
---- Начинается с индекса 0, заканчивается с индексом 30
Явное лучше, чем неявное.
---- Начинается с индекса 31, заканчивается на индексе 64
Лучше простое, чем сложное.
---- Начинается с индекса 65, заканчивается на индексе 95
Следующие шаги
Хотите создать свою собственную систему классификации текстов? Ознакомьтесь с руководством по классификаторам.
Хотите использовать другую реализацию тега POS или блокировку именных фраз? Ознакомьтесь с руководством по расширенному использованию.
Функция полярности— RDocumentation
Примеры
# NOT RUN {
с (ДАННЫЕ, полярность (состояние, список (пол, взрослый)))
(poldat <- with (sentSplit (ДАННЫЕ, 4), полярность (состояние, лицо)))
считает (полдат)
баллы (полдат)
сюжет (полдат)
poldat2 <- с (mraja1spl, полярность (диалог,
list (sex, fam.aff, умер)))
colsplit2df (баллы (poldat2))
сюжет (poldat2)
сюжет (баллы (poldat2))
накопительный (poldat2)
poldat3 <- с (rajSPLIT, полярность (диалог, человек))
poldat3 [["группа"]] [, "OL"] <- outlier_labeler (scores (poldat3) [,
"пр.полярность "])
poldat3 [["все"]] [, "OL"] <- outlier_labeler (counts (poldat3) [,
"полярность"])
htruncdf (баллов (poldat3), 10)
htruncdf (считает (poldat3), 15, 8)
сюжет (poldat3)
сюжет (poldat3, nrow = 4)
qheat (scores (poldat3) [, -7], high = "красный", order.b = "ave.polarity")
## Создание настроенного исследователем sentiment.frame
POLKEY <- кадр_положения (положительные.слова, отрицательные.слова)
ПОЛКЕЙ
c («абразивный», «резкий», «счастливый»)% hl% POLKEY
# Расширение sentiment.frame
mycorpus <- c («Вау, это грубый ход.», «Его шутки такие банальные»)
отсчетов (полярность (микорпус))
POLKEY <- кадр_положения (c (положительный.слова, «сырые»), с (отрицательные. слова, «банально»))
подсчитывает (полярность (микорпус, полярность.frame = POLKEY))
## АНИМАЦИЯ
# ===========
(deb2 <- with (subset (pres_debates2012, time == "time 2"),
полярность (диалог, лицо)))
bg_black <- Animate (deb2, нейтральный = "белый", current.speaker.color = "grey70")
печать (bg_black, пауза = 0,75)
bgb <- vertex_apply (bg_black, label.color = "grey80", size = 20, color = "grey40")
bgb <- edge_apply (bgb, label.color = "yellow")
print (bgb, bg = "черный", пауза = 0,75)
## Сохрани это
библиотека (анимация)
библиотека (igraph)
библиотека (plotrix)
loc <- папка (animation_polarity)
## Настройте функцию построения графика
oopt <- анимация :: ani.варианты (интервал = 0,1)
FUN <- function () {
Название <- «Анимированные полярности: президентские дебаты 2012 года 2»
Легенда <- c (-1.1, -1.25, -.2, -1.2)
Legend.cex <- 1
lapply (seq_along (bgb), function (i) {
par (mar = c (2, 0, 1, 0), bg = "черный")
набор.семян (10)
plot.igraph (bgb [[i]], edge.curved = TRUE)
mtext (Заголовок, сторона = 3, col = "white")
color.legend (Легенда [1], Легенда [2], Легенда [3], Легенда [4],
c ("Отрицательный", "Нейтральный", "Положительный"), атрибуты (bgb) [["legend"]],
cex = Легенда.cex, col = "white")
анимация :: ani.pause ()
})
}
ВЕСЕЛЬЕ()
## Определить ОС
type <- if (.Platform $ OS.type == "windows") оболочка else system
saveHTML (FUN (), autoplay = FALSE, loop = TRUE, verbose = FALSE,
ani.height = 500, ani.width = 500,
outdir = file.path (loc, "новый"), single.opts =
"'control': ['first', 'play', 'loop', 'speed'], 'delayMin': 0")
## Определить ОС
type <- if (.Platform $ OS.type == "windows") оболочка else system
saveHTML (FUN (), autoplay = FALSE, loop = TRUE, verbose = FALSE,
ани.height = 1000, ani.width = 650,
outdir = loc, single.opts =
"'control': ['first', 'play', 'loop', 'speed'], 'delayMin': 0")
## Анимированный соответствующий текстовый сюжет
Animate (deb2, type = "текст")
# ===================== #
## Сложная анимация ##
# ===================== #
библиотека (анимация)
библиотека (сетка)
библиотека (gridBase)
библиотека (qdap)
библиотека (qdapTools)
библиотека (igraph)
библиотека (plotrix)
библиотека (gridExtra)
deb2dat <- subset (pres_debates2012, time == "time 2")
deb2dat [, "человек"] <- фактор (deb2dat [, "человек"])
(deb2 <- с (deb2dat, полярность (диалог, человек)))
## Настроить сетевую версию
bg_black <- Animate (deb2, нейтральный = "белый", текущий.динамик.color = "grey70")
bgb <- vertex_apply (bg_black, label.color = "grey80", size = 30, label.size = 22,
color = "grey40")
bgb <- edge_apply (bgb, label.color = "yellow")
## Настроить версию бара
deb2_bar <- Animate (deb2, as.network = FALSE)
## Создать папку
loc2 <- папка (animation_polarity2)
## Настройте функцию построения графика
oopt <- animation :: ani.options (интервал = 0,1)
FUN2 <- function (follow = FALSE, theseq = seq_along (bgb)) {
Название <- «Анимированные полярности: президентские дебаты 2012 года 2»
Легенда <- c (.2, -1,075, 1,5, -1,005)
Legend.cex <- 1
lapply (theseq, function (i) {
if (следовать) {
png (file = sprintf ("% s / images / Rplot% s.png", loc2, i),
ширина = 650, высота = 725)
}
## Настройте макет
макет (матрица (c (rep (1, 9), rep (2, 4)), 13, 1, byrow = TRUE))
## Сюжет 1
par (mar = c (2, 0, 2, 0), bg = "черный")
#par (mar = c (2, 0, 2, 0))
набор. семян (20)
plot.igraph (bgb [[i]], edge.curved = TRUE)
mtext (Заголовок, сторона = 3, col = "white")
цвет.легенда (Легенда [1], Легенда [2], Легенда [3], Легенда [4],
c ("Отрицательный", "Нейтральный", "Положительный"), атрибуты (bgb) [["legend"]],
cex = Legend.cex, col = "white")
## Plot2
plot.new ()
vps <- baseViewports ()
uns <- unit (c (-1,3, .5, -. 75, .25), "см")
p <- deb2_bar [[i]] +
тема (plot.margin = uns,
text = element_text (color = "white"),
plot.background = element_rect (fill = "черный",
цвет = "черный"))
print (p, vp = vpStack (vps $ figure, vps $ plot))
анимация :: ани.Пауза()
if (следовать) {
dev.off ()
}
})
}
FUN2 ()
## Определить ОС
type <- if (.Platform $ OS.type == "windows") оболочка else system
saveHTML (FUN2 (), autoplay = FALSE, loop = TRUE, verbose = FALSE,
ani.height = 1000, ani.width = 650,
outdir = loc2, single.opts =
"'control': ['first', 'play', 'loop', 'speed'], 'delayMin': 0")
FUN2 (ИСТИНА)
# ===================== #
библиотека (анимация)
библиотека (сетка)
библиотека (gridBase)
библиотека (qdap)
библиотека (qdapTools)
библиотека (igraph)
библиотека (plotrix)
библиотека (графики)
deb2dat <- subset (pres_debates2012, time == "time 2")
deb2dat [, "человек"] <- фактор (deb2dat [, "человек"])
(deb2 <- с (deb2dat, полярность (диалог, человек)))
## Настроить сетевую версию
bg_black <- Animate (deb2, нейтральный = "белый", текущий.динамик.color = "grey70")
bgb <- vertex_apply (bg_black, label.color = "grey80", size = 30, label.size = 22,
color = "grey40")
bgb <- edge_apply (bgb, label.color = "yellow")
## Настроить версию бара
deb2_bar <- Animate (deb2, as.network = FALSE)
## Настроить версию строки
deb2_line <- график (накопительный (deb2_bar))
## Создать папку
loc2b <- папка (animation_polarity2)
## Настройте функцию построения графика
oopt <- animation :: ani.options (интервал = 0,1)
FUN2 <- function (follow = FALSE, theseq = seq_along (bgb)) {
Название <- «Анимированные полярности: президентские дебаты 2012 года 2»
Легенда <- c (.2, -1,075, 1,5, -1,005)
Legend.cex <- 1
lapply (theseq, function (i) {
if (следовать) {
png (file = sprintf ("% s / images / Rplot% s.png", loc2b, i),
ширина = 650, высота = 725)
}
## Настройте макет
макет (матрица (c (rep (1, 9), rep (2, 4)), 13, 1, byrow = TRUE))
## Сюжет 1
par (mar = c (2, 0, 2, 0), bg = "черный")
#par (mar = c (2, 0, 2, 0))
набор. семян (20)
plot.igraph (bgb [[i]], edge.curved = TRUE)
mtext (Заголовок, сторона = 3, col = "white")
цвет.легенда (Легенда [1], Легенда [2], Легенда [3], Легенда [4],
c ("Отрицательный", "Нейтральный", "Положительный"), атрибуты (bgb) [["legend"]],
cex = Legend.cex, col = "white")
## Plot2
plot.new ()
vps <- baseViewports ()
uns <- unit (c (-1,3, .5, -. 75, .25), "см")
p <- deb2_bar [[i]] +
тема (plot.margin = uns,
text = element_text (color = "white"),
plot.background = element_rect (fill = "черный",
цвет = "черный"))
print (p, vp = vpStack (vps $ figure, vps $ plot))
анимация :: ани.Пауза()
if (следовать) {
dev.off ()
}
})
}
FUN2 ()
## Определить ОС
type <- if (.Platform $ OS.type == "windows") оболочка else system
saveHTML (FUN2 (), autoplay = FALSE, loop = TRUE, verbose = FALSE,
ani.height = 1000, ani.width = 650,
outdir = loc2b, single.opts =
"'control': ['first', 'play', 'loop', 'speed'], 'delayMin': 0")
FUN2 (ИСТИНА)
## Повышенная сложность
## --------------------
## Вспомогательная функция для привязки ggplots
cbinder <- function (x, y) {
uns_x <- unit (c (-1.3, .15, -. 75, .25), «см»)
uns_y <- unit (c (-1,3, .5, -. 75, .15), "см")
x <- x + theme (plot.margin = uns_x,
text = element_text (color = "white"),
plot.background = element_rect (fill = "черный",
цвет = "черный")
)
y <- y + theme (plot.margin = uns_y,
text = element_text (color = "white"),
plot.background = element_rect (fill = "черный",
цвет = "черный")
)
графики <- list (x, y)
grobs <- список ()
высоты <- список ()
for (я в 1: длина (участки)) {
grobs [[i]] <- ggplotGrob (графики [[i]])
heights [[i]] <- grobs [[i]] $ heights [2: 5]
}
maxheight <- делать.вызов (grid :: unit.pmax, heights)
for (i in 1: length (grobs)) {
grobs [[i]] $ heights [2: 5] <- as.list (maxheight)
}
do.call ("аранжировкаGrob", c (grobs, ncol = 2))
}
deb2_combo <- Карта (cbinder, deb2_bar, deb2_line)
## Создать папку
loc3 <- папка (animation_polarity3)
FUN3 <- function (follow = FALSE, theseq = seq_along (bgb)) {
Название <- «Анимированные полярности: президентские дебаты 2012 года 2»
Легенда <- c (.2, -1.075, 1.5, -1.005)
Legend.cex <- 1
lapply (theseq, function (i) {
if (следовать) {
png (file = sprintf ("% s / images / Rplot% s.png ", loc3, i),
ширина = 650, высота = 725)
}
## Настройте макет
макет (матрица (c (rep (1, 9), rep (2, 4)), 13, 1, byrow = TRUE))
## Сюжет 1
par (mar = c (2, 0, 2, 0), bg = "черный")
#par (mar = c (2, 0, 2, 0))
набор. семян (20)
plot.igraph (bgb [[i]], edge.curved = TRUE)
mtext (Заголовок, сторона = 3, col = "white")
color.legend (Легенда [1], Легенда [2], Легенда [3], Легенда [4],
c ("Отрицательный", "Нейтральный", "Положительный"), атрибуты (bgb) [["legend"]],
cex = Легенда.cex, col = "white")
## Plot2
plot.new ()
vps <- baseViewports ()
p <- deb2_combo [[i]]
print (p, vp = vpStack (vps $ figure, vps $ plot))
анимация :: ani.pause ()
if (следовать) {
dev.off ()
}
})
}
FUN3 ()
type <- if (.Platform $ OS.type == "windows") оболочка else system
saveHTML (FUN3 (), autoplay = FALSE, loop = TRUE, verbose = FALSE,
ani.height = 1000, ani.width = 650,
outdir = loc3, single.opts =
"'control': ['first', 'play', 'loop', 'speed'], 'delayMin': 0")
FUN3 (ИСТИНА)
## ----------------------------- ##
## Ограничение между -1 и 1 ##
## ----------------------------- ##
## Старое поведение полярности ограничивало выходное значение от -1 до 1
## это может быть воспроизведено с помощью аргумента `constrain = TRUE`:
полярность («действительно ненавижу гнев»)
полярность ("действительно ненавижу гнев", ограничить = ИСТИНА)
# ================== #
## Статическая сеть ##
# ================== #
(poldat <- with (sentSplit (ДАННЫЕ, 4), полярность (состояние, лицо)))
m <- Сеть (poldat)
м
print (m, bg = "grey97", vertex.color = "grey75")
print (m, title = "Карта дискурса полярности", title.color = "white", bg = "black",
legend.text.color = "белый", vertex.label.color = "grey70",
edge.label.color = "желтый")
## или используйте темы:
dev.off ()
m + qtheme ()
м + theme_nightheat
dev.off ()
m + theme_nightheat (title = "Карта дискурса полярности")
# =============================== #
## ПРИМЕР КУМУЛЯТИВНОЙ ПОЛЯРНОСТИ ##
# =============================== #
# Гедонометрика #
# =============================== #
poldat4 <- с (rajSPLIT, полярность (диалог, действие, ограничение = ИСТИНА))
polcount <- na.опустить (считает (poldat4) $ полярность)
len <- длина (polcount)
cummean <- функция (x) {cumsum (x) / seq_along (x)}
cumpolarity <- data.frame (cum_mean = cummean (polcount), Time = 1: len)
## Расчет прямоугольников фона
заканчивается <- cumsum (rle (counts (poldat4) $ act) $ lengths)
начинается <- c (1, head (заканчивается + 1, -1))
rects <- data.frame (xstart = начинается, xend = заканчивается + 1,
Act = c («I», «II», «III», «IV», «V»))
библиотека (ggplot2)
ggplot () + theme_bw () +
geom_rect (данные = rects, aes (xmin = xstart, xmax = xend,
ymin = -Inf, ymax = Inf, fill = Act), alpha = 0.17) +
geom_smooth (данные = cumpolarity, aes (y = cum_mean, x = время)) +
geom_hline (y = mean (polcount), color = "grey30", size = 1, alpha = .3, linetype = 2) +
annotate ("текст", x = среднее значение (заканчивается [1: 2]), y = среднее значение (polcount), color = "grey30",
label = "Средняя полярность", vjust = .3, size = 3) +
geom_line (данные = cumpolarity, aes (y = cum_mean, x = время), size = 1) +
ylab («Кумулятивная средняя полярность») + xlab («Продолжительность») +
scale_x_continuous (развернуть = c (0,0)) +
geom_text (данные = rects, aes (x = (xstart + xend) / 2, y = -.04,
label = paste ("Акт", Акт)), размер = 3) +
направляющие (заполнить = ЛОЖЬ) +
scale_fill_brewer (palette = "Set1")
#}
nlp - Ошибка получения ключа = 0 при вычислении полярности в Python
У меня есть две колонки - текст и заголовок для новостных статей.
Данные выглядят нормально, извиняюсь за печатный экран, просто чтобы показать структуру.
Но при попытке вычислить полярность выдает странную ошибку.
# Create
полярность = []
# Создать цикл только для текстового столбца
для i в диапазоне (len (jordan_df ['text'])):
полярность.append (TextBlob (jordan_df ['text'] [i]). sentiment.polarity)
# Собираем данные
polarity_data = {'article_text': jordan_df ['text'], 'article_polarity': полярность}
Странно то, что этот код работает, когда я меняю jordan_df на some_df с той же структурой.
Ошибка:
KeyError Traceback (последний вызов последним)
/usr/local/lib/python3.7/dist-packages/pandas/core/indexes/base.py в get_loc (self, key, method,
толерантность)
2897 попыток:
-> 2898 вернуть себе._engine.get_loc (casted_key)
2899, кроме KeyError как err:
pandas / _libs / index.pyx в pandas._libs.index.IndexEngine.get_loc ()
pandas / _libs / index.pyx в pandas._libs.index.IndexEngine.get_loc ()
pandas / _libs / hashtable_class_helper.pxi в pandas._libs.hashtable.Int64HashTable.get_item ()
pandas / _libs / hashtable_class_helper.pxi в pandas._libs.hashtable.Int64HashTable.get_item ()
** KeyError: 0 **
Вышеупомянутое исключение явилось прямой причиной следующего исключения:
KeyError Traceback (последний вызов последним)
3 кадра
в <модуль> ()
9 # Создать цикл только для текстового столбца
10 для i в диапазоне (len (jordan_df ['text'])):
---> 11 полярность.append (TextBlob (jordan_df ['text'] [i]). sentiment.polarity)
12
13 # Собираем данные
/usr/local/lib/python3.7/dist-packages/pandas/core/series.py в __getitem __ (сам, ключ)
880
881 элиф key_is_scalar:
-> 882 вернуть self._get_value (ключ)
883
884, если is_hashable (ключ):
/usr/local/lib/python3.7/dist-packages/pandas/core/series.py в _get_value (self, label, takeable)
988
989 # Аналогично Index.get_value, но мы не возвращаемся к позиционному
-> 990 loc = self.index.get_loc (метка)
991 вернуть self.index._get_values_for_loc (self, loc, label)
992
/usr/local/lib/python3.7/dist-packages/pandas/core/indexes/base.py в get_loc (self, key, method,
толерантность)
2898 вернуть self._engine.get_loc (casted_key)
2899, кроме KeyError как err:
-> 2900 поднять KeyError (ключ) из err
2901
2902, если допуск не равен Нет:
Взаимное ингибирование между PTEN и PIP3 создает бистабильность полярности в подвижных клетках
Культура клеток
Dictyostelium discoideum штамм Ax2 дикого типа (идентификатор штамма dictyBase: DBS0235518), любезный подарок М.Маэда использовалась в качестве родительской клеточной линии на протяжении всего исследования. Штамм pi3k1-5 -null (ID штамма dictyBase: DBS0252652) был любезным подарком от Р. Кея (MRC, Кембридж, Великобритания). Все клеточные линии выращивали в среде HL5 (15,4 г глюкозы, 7,15 г дрожжевого экстракта, 14,3 г протеозопептона № 2, 0,485 г KH 2 PO 4 , 1,28 г Na 2 HPO 4 12H 2 O, 0,2 мг фолиевой кислоты, 0,06 мг цианокобаламина на л) с добавлением пенициллина и стрептомицина при 21 ° C.
Конструирование клеточных линий
Нулевую клеточную линию pten получали путем гомологичной рекомбинации. Была изготовлена конструкция для нокаута гена, которая состояла из 5'- и 3'-фрагментов гена pten (GenBank: AF483827.1), в которые вмешалась кассета экспрессии для гена устойчивости к бластицидину. 5'- и 3'-фрагменты были амплифицированы из геномной ДНК D. discoideum с помощью ПЦР с использованием праймеров DdPTEN-KO1 и DdPTEN-KO2, а также DdPTEN-KO3 и DdPTEN-KO4, перечисленных в дополнительной таблице 2, соответственно.Весь конструкт амплифицировали с помощью ПЦР слияния с использованием амплифицированных фрагментов и кассеты, которую вводили в штамм Ax2 дикого типа D. discoideum путем электропорации. Для клеточных линий, экспрессирующих PI3K с постоянной мембраной, ген, кодирующий myrPI3K2, в котором PI3K2 был на N-конце конъюгирован с 16 аминокислотами из куриного c-Src, амплифицировали с помощью ПЦР с использованием праймеров PI3K2-1, PI3K2-2 и PI3K2. -3 и клонирован в сайты AatII и SpeI во внехромосомной плазмиде, pHK12bla 10 .Последовательность из 16 аминокислот была MGSSKSKPKDPSQRRR, которая составляет сигнал миристоилирования и основные аминокислоты, достаточные для стабильной мембранной ассоциации. Конструкцию вводили в клетки путем электропорации. Эти трансформанты были отобраны с концентрацией 10 мкг / мл бластицидина -1 S. Для одновременной экспрессии PTEN-Halo и PH PKB -eGFP, ген, кодирующий DdPTEN-, DdPTEN G129E - или HsPTEN-Halo, был амплифицирован с помощью ПЦР с использованием праймеров DdPTEN-OE1 и DdPTEN-OE2 и HsPTEN-OE1 и HsPTEN-OE2 и клонирование в сайты BglII и SpeI pDM344 56 (GenBank: FJ402941).В гене, кодирующем белок HaloTag, сайт NgoMIV был удален путем синонимичной замены, которая была введена посредством сайт-направленного мутагенеза (Stratagene). Расщепленный NgoMIV фрагмент pDM344, состоящий из промотора actin15, гена PTEN-Halo и терминатора actin8, был клонирован в сайт NgoMIV внехромосомной плазмиды pDM181, в котором ген, кодирующий PH PKB -eGFP, был клонирован в BglII и Сайты XbaI. Плазмиду вводили в клетки электропорацией, и трансформанты отбирали под 20 мкг мл -1 Geneticine.Для индуцированной доксициклином экспрессии конститутивно активных форм малых G-белков ген, кодирующий RasG Q61L , RasC Q62L или Rap1 G12V , был клонирован в сайты BglII и SpeI внехромосомной плазмиды pDM359 (GenBank: EU6). Плазмиду вводили в клетки путем электропорации, и трансформанты отбирали с концентрацией 40 мкг / мл. -1 гигромицин B.
Подготовка клеток для микроскопии
Культивируемые клетки голодали перед микроскопическим наблюдением следующим образом.Клетки дважды промывали буфером для развития (DB; 5 мМ Na / KPO 4 , 2 мМ MgSO 4 , 0,2 мМ CaCl 2 , pH 6,5) центрифугированием при 500 × g в течение 2 мин. В случае клеточных линий, экспрессирующих myrPI3K2, 5 мл клеточной суспензии при 1 × 10 6 клеток мл -1 переносили в колбу на 20 мл и встряхивали при 150 об / мин в течение 4 ч при 21 ° C. В случае других клеточных линий 1 мл клеточной суспензии из расчета 3 × 10 6 клеток на мл переносили в 35-мм культуральную чашку и выдерживали в течение 4 часов при 21 ° C.В течение последних 30 минут лиганд HaloTag TMR (Promega) был добавлен к суспензии клеток в конечной концентрации 2 мкМ и 20 нМ для визуализации субклеточной локализации и визуализации одиночных молекул, соответственно. После инкубации клетки дважды промывали DB посредством центрифугирования и суспендировали в DB в количестве примерно 5 × 10 6 клеток на мл.
Визуализация миграции клеток
Концентрация 10 мкл суспензии голодных клеток была помещена на покровное стекло чашки со стеклянным дном 35 мм (стекло диаметром 27 мм, Iwaki).Клеткам давали возможность прилипнуть к поверхности в течение 10-минутной инкубации, заполняли 1 мл DB и давали возможность отстояться еще одной инкубацией в течение не менее 20 минут. Клетки наблюдали под инвертированным микроскопом (IX71, Olympus), снабженным покадровой камерой (DS-2MBW, Nikon). Чтобы стимулировать клетки пространственным градиентом цАМФ, DB, содержащую 1 мМ цАМФ, заполненную стеклянной микропипеткой (Femtotips II, Eppendorf), высвобождали путем нанесения 50 гПа с использованием FemtoJet (Eppendorf). Изображения были получены с интервалом времени от 1 до 5 с в течение 30 мин.
Визуализация субклеточной локализации
Чтобы наблюдать спонтанную динамику PTEN и PIP3, 200–300 мкл суспензии голодных клеток в DB, содержащей 5 мкМ латрункулина A (Sigma) и 4 мМ кофеина, помещали на покровное стекло 35-мм стекла. нижняя тарелка (стекло диаметром 12 мм, Иваки). Клеткам давали возможность осесть на 30-минутную инкубацию, а затем наблюдали с помощью лазерной конфокальной микроскопии (A1, Nikon или FV-1000, OLYMPUS). Изображения были получены с интервалом времени 5 с в течение 30 мин.
Чтобы наблюдать реакцию на манипуляции с активностью PI3K, 15 мкл суспензии голодных клеток в DB, содержащей 10 мкМ латрункулина A, помещали на покровное стекло чашки со стеклянным дном 35 мм (стекло диаметром 12 мм, Iwaki). . Клеткам давали возможность осесть в течение 30 мин инкубации, а затем наблюдали под лазерной конфокальной микроскопией. Начинали покадровую визуализацию, и в то же время к суспензии клеток добавляли 5 мкл DB, содержащего 10 мкМ латрункулина A и 160 мкМ LY294002 (Cayman Chemical), для обработки клеток LY294002 в конечной концентрации 40 мкМ.Каждые 3 минуты к суспензии клеток добавляли 5, 25, 50, 100, 200 или 400 мкл DB, содержащего 10 мкМ латрункулина A, для серийного разбавления LY294002 до 32, 16, 8, 4, 2 и 1 мкМ.
Для наблюдения PTEN и PIP3 в клеточных линиях, экспрессирующих конститутивно активные формы малых G-белков, 300 мкл суспензии голодных клеток в DB, содержащей 10 мкМ латрункулина A, помещали на покровное стекло 35-мм чашки со стеклянным дном (12- стекло диаметром мм, Иваки). Клеткам давали возможность осесть после 30-минутной инкубации.Затем добавляли 100 мкл DB, содержащего 10 мкМ латрункулина A и 40 мкг / мл доксициклина -1 (гидрохлорид доксициклина, MP Biomedicals), и клетки инкубировали еще 45 мин и, наконец, наблюдали под лазерной конфокальной микроскопией.
Чтобы наблюдать PTEN и PIP3 в ответ на градиент хемоаттрактанта, 300 мкл суспензии голодных клеток в DB, содержащей 5 мкМ латрункулина A, помещали на покровное стекло чашки со стеклянным дном 35 мм (стекло диаметром 12 мм, Iwaki ). Клеткам давали возможность осесть после 10-минутной инкубации.Затем добавляли 2000 мкл DB, содержащего 5 мкМ латрункулина A, и клетки инкубировали еще 20 мин и, наконец, наблюдали под лазерной конфокальной микроскопией. DB, содержащую 10 мкМ цАМФ, помещенную в стеклянную микропипетку (Femtotips, Eppendorf), высвобождали путем нанесения 50 гПа с использованием FemtoJet. Изображения получали каждые 5 с, а 12 изображений после 1-2 мин применения градиента усреднялись и использовались для анализа.
Визуализация одиночных молекул
10 мкл суспензии голодных клеток помещали на покровное стекло, очищенное ультразвуком в 0.1 н. КОН в течение 30 мин и дважды промывали поочередно 99,5% этанолом (особой чистоты) и дистиллированной водой перед использованием. Клеткам давали возможность прикрепиться к поверхности, инкубируя покровное стекло во влажной камере в течение 10 мин. Клетки покрывали листом агарозы, который представлял собой 2% агарозу М (Amersham Pharmacia Biotech) в DB без Ca 2+ или Mg 2+ , растворенных в микроволновой печи и затвердевших между двумя стеклянными предметными стеклами, расположенными между покровными стеклами. Лишнюю жидкость удалили фильтровальной бумагой.После инкубации во влажной камере в течение не менее 20 минут покровное стекло помещали в камеру для клеток Attofluor TM (ThermoFisher Scientific) и наблюдали в режиме TIRFM. Для обработки ингибитором для суспензии клеток использовали DB, содержащий 5–10 мкМ латрункулина A (Sigma) и 40 мкМ LY294002 (Cayman Chemical), и агарозный лист размером 1 см 2 , пропитанный DB, содержащим ингибиторы, в течение не менее 30 мин. используется для наложения. Одиночные молекулы PTEN-Halo, меченные TMR, наблюдались под объективом TIRFM, сконструированным на инвертированном флуоресцентном микроскопе (IX70, Olympus) 57 .Изображения были получены со скоростью 30 кадров в секунду. Для количественной оценки частоты ассоциации с мембраной последовательно выполняли визуализацию одиночных молекул и флуоресцентную визуализацию EPI в одних и тех же клетках под разными углами падения возбуждающего света, достигнутыми путем наклона зеркала на пути света.
Биохимический анализ субклеточной локализации
1200 мкл суспензии голодных клеток при 1 × 10 7 клеток на мл смешивали с 300 мкл DB, содержащего 50 мкМ латрункулина A, в 15-мл пробирке и инкубировали при встряхивании при 150 об.вечера. на 30 мин. Этот шаг был продублирован. В течение последних 5 минут к одному образцу добавляли 20 мкл DB, содержащего 4,5 мМ LY294002. После центрифугирования при 500 × g в течение 2 минут супернатант удаляли, и клетки повторно суспендировали в 150 мкл DB. 100 мкл клеточной суспензии немедленно смешивали со 100 мкл базального буфера (20 мМ Трис-HCl, 2 мМ MgSO 4 , pH 8,0) в предварительно охлажденном шприце (1 мл, Terumo), и клеточный лизат пропускали через два слоя. мембраны (трековая мембрана Whatman Nuclepore, размер пор 5.0 мкм, Sigma-Aldrich) собирали в пробирку на льду. 108 мкл лизата переносили в новую пробирку на льду и центрифугировали при 16000 × g в течение 1 мин при 4 ° C. Концентрацию 36 мкл супернатанта переносили в новую пробирку, содержащую 12 мкл 4 × буфера для образца (с добавлением β-меркаптоэтанола, Wako). Остаточный супернатант удаляли, а осадок суспендировали в 48 мкл 1 × буфера для образцов. Фракции супернатанта и осадка кипятили в течение 5 мин и хранили при -30 ° C. 10 мкл образцов подвергали SDS-PAGE в готовом геле (SuperSep Ace 5–20%, Wako) и наносили на мембрану PVDF (Immobilon-P, Millipore).Для вестерн-блоттинга PTEN-Halo мембрану обрабатывали 5% (мас. / Об.) Обезжиренным молоком / TBS-T (трис-буферный солевой раствор, содержащий 0,05% твин-20) в течение 1 ч при комнатной температуре (RT), промывали TBS-T и реагировали с мышиным моноклональным антителом против HaloTag (G921A, Promega), разведенным TBS-T в соотношении 1: 1000 в течение 1 ч при комнатной температуре. Мембрану промывали TBS-T и подвергали взаимодействию с конъюгированным с пероксидазой хрена (HRP) антимышиным IgG (NA931, GE Healthcare), разведенным TBS-T при 1: 50000 в течение 1 часа при комнатной температуре. После промывания TBS-T сигналы детектировались с помощью ECL Prime (GE Healthcare).Для анализа PH PKB -eGFP антитела на мембране удаляли промыванием TBS-T, и мембрану обрабатывали 5% обезжиренным молоком / TBS-T в течение 1 ч при комнатной температуре и повторно зондировали анти-GFP. pAb-HRP-DirecT (598-7, MBL), разбавленный 1% обезжиренного молока / TBS в соотношении 1: 2000 в течение 1 ч при комнатной температуре.
Анализ миграции клеток
Координаты x и y -координаты клетки в фильме были определены полуавтоматически с использованием программного обеспечения, созданного в лаборатории, и была построена 30-минутная траектория миграции, состоящая из 361 положения на интервал 5 с 58 (дополнительные рис.1b и 2ab). Смещение клетки измеряли каждые 5 с и умножали на 12 для расчета мгновенной скорости миграции клеток (мкм мин -1 ). Измерение мгновенной скорости из более чем 50 ячеек, каждая из которых имеет 360 значений, дало сводку среднего и пятизначного числа, которая включала минимум, нижний квартиль, медиану, верхний квартиль и максимум, как показано на графике прямоугольных усов ( Рис. 1f; Дополнительная таблица 1). Для количественной оценки индекса хемотаксии траектория была перемещена таким образом, чтобы положение клетки на t = 0 было расположено в исходной точке, а положение кончика микропипетки, высвобождающего цАМФ, было расположено на оси y ( x ). = 0, y > 0) (Дополнительный рис.2а, б). Среднее значение y-компонента 5-секундного смещения было разделено на 5-секундное смещение в двух измерениях (2D), что дало хемотаксический индекс клетки (дополнительная таблица 1). Точное значение n , которое представляет собой количество проанализированных клеток, можно найти в дополнительной таблице 1.
Анализ субклеточной локализации
Анализ изображений пространственно-временной динамики обогащения PTEN и PIP3 на клеточной мембране был выполнен на основе кимографы, полученные с помощью макроса в Image-Pro Plus 15 (Media Cybernetics) (рис.1h, k; Дополнительный рис. 1c-e). Интенсивности флуоресценции PTEN-Halo-TMR и PH PKB -eGFP измеряли по периферии круговой области интереса, установленной на изображении клетки. Диаметр области интереса оставался постоянным для набора из 361 изображения, полученного с 5-секундными интервалами в течение 30 минут. Все клетки, которые показали значительную экспрессию как PTEN-Halo-TMR, так и PH PKB -eGFP, были использованы для измерения, и были проанализированы несколько наборов, полученных в ходе экспериментов, проведенных в разные дни.Расчеты автокорреляции, периода колебаний и усредненного распределения интенсивности по периферии клетки были выполнены с использованием MATLAB (MathWorks) (рис. 1m – o; дополнительный рис. 2d). Данные представлены как средние значения ± стандартное отклонение. Точное значение n , которое представляет собой количество проанализированных ячеек, можно найти в разделе «Результаты» и в подписях к рисункам.
Для анализа взаимного ингибирующего отношения между уровнями PTEN и PIP3 на клеточной мембране, интенсивности флуоресценции PTEN-Halo-TMR и PH PKB -eGFP были измерены с использованием команды построения профиля против круговой линии, установленной на периферии изображение ячейки в ImageJ (рис.2; Дополнительный рис. 3b – d, 4a, c, d, f). Типичная периферия клетки, наблюдаемая под лазерной конфокальной микроскопией, составляла приблизительно 30 мкм, что соответствует 300 пикселям в изображении 1024 x 1024 пикселя, полученном с помощью объектива 60 x и 2-кратного оптического увеличения Nikon A1. Измерения в каналах TMR и GFP в пределах одной и той же микроскопической области интереса дали примерно 300 наборов данных об интенсивности TMR и GFP по периферии. Интенсивности TMR и GFP были нормализованы к средним значениям TMR и GFP, измеренным в цитоплазме, соответственно.Наборы данных, полученные из 5 репрезентативных ячеек, были отображены на графике рассеяния тепла, на котором единый набор данных нормализованных интенсивностей TMR и GFP представлен одной точкой, нанесенной на плоскость PTEN-PIP3. Одни и те же клетки анализировали во время манипуляции с концентрацией LY294002. Гистограмма нанесенных точек на плоскости PTEN-PIP3 использовалась для расчета распределения плотности вероятности в 2D, которое отображается в виде тепловой карты. Две тепловые карты LY294002 с концентрацией 1 и 40 мкМ соответственно были подогнаны к двумерному гауссовскому распределению для создания контуров изоплотности, которые использовались для оценки границы между двумя распределениями (дополнительный рис.3в). Графики рассеяния тепла и тепловые карты были сделаны с использованием MATLAB. Точное значение n , которое представляет собой количество проанализированных ячеек, можно найти в разделе «Результаты» и в подписях к рисункам.
Для анализа временных изменений субклеточной локализации при добавлении / разбавлении LY294002 или цАМФ, интенсивности флуоресценции на клеточной мембране или в цитоплазме были измерены и нормализованы к средней интенсивности флуоресценции, измеренной до лечения (рис. 3c, d; Дополнительные рис.2д, 3а). Данные представлены в виде средних значений ± стандартное отклонение. Точное значение n , которое представляет собой количество проанализированных ячеек, можно найти в подписях к рисункам.
Отслеживание одиночной молекулы
Траектория одиночной молекулы PTEN-Halo-TMR, подвергающейся латеральной диффузии на клеточной мембране, была получена полуавтоматически с использованием лабораторного программного обеспечения 35,59 . Координаты молекулы x и y определяли путем подгонки распределения интенсивности флуоресценции к двумерному гауссовскому распределению каждые 33 мсек.Все молекулы, обнаруженные в фильме, отслеживались, когда это было возможно, а те, которые можно было обнаружить в начале и в конце фильма, исключались из анализа. Ансамбль из N траекторий, выбранных в тех же экспериментальных условиях, был обозначен как ( x i ( t ), y i ( t )), где i = 1, 2,… N и t = 0 означает время, когда на мембране появилась i -я молекула.Точные значения N и n , которые представляют собой количество анализируемых траекторий и ячеек, соответственно, можно найти в Таблице 1.
Анализ времени жизни одной молекулы
Число молекул было подсчитано при t ( t = 0, 0,33, 0,66, 0,10,…) и определяется как N при t = 0. Число, деленное на N , было построено вдоль t , чтобы построить кривую диссоциации (рис. 4c ). Данные на рис. 4c представлены как средние.{- \ left ({k_j + k _ {\ mathrm {b}}} \ right) t}}, $$
(1)
, где k j обозначает j -ю константу скорости распада, а k b обозначает константу скорости фотообесцвечивания TMR. Поскольку кривая диссоциации затухает быстрее, чем фотообесцвечивание, она отражает кинетику мембранной диссоциации PTEN. Кривая диссоциации перед t = 7 с была хорошо подогнана к уравнению (1) с J = 3 и соответствовала количеству состояний связывания с мембраной 25 (таблица 1).D} = 1. $$
(3)
D j и q D j обозначают коэффициент диффузии и долю j -го компонента ( j = 1, 2,… Дж ) соответственно. ε обозначает стандартное отклонение ошибки измерения, которое было оценено как менее 23 нм с помощью линейной регрессии средних квадратов смещений с временем запаздывания τ = 0.033 или 0,066 с с использованием уравнения 35 MSD ( τ ) = 4 Dτ + 4 ε 2 . D j и q D j с переменной J ( J = 1,2,3,4) были оценены методом максимального правдоподобия (MLE) с использованием M образцов Δ r m ( m = 1, 2,… M ), измеренных по N траекториям.Модель, предполагающая три компонента ( J = 3), наиболее вероятно была основана на информационном критерии Акаике (AIC) 35 (рис. 5a; таблица 1). AIC модели, предполагающей компоненты J , AIC J , описывается как
$$ {\ mathrm {AIC}} _ J = - 2L_J \ left ({\ hat \ theta _J} \ right) + \ left ({2J - 1} \ right) \ log \ left ({\ log M} \ right), $$
(4)
, где θ J = ( D j , q D j ) ( j = 1, 2,… ) обозначает вектор параметров, которые необходимо оценить, а L J обозначает логарифмическую вероятность, записанную как
$$ L_J \ left ({\ theta _J} \ right) = \ mathop {\ sum} \ limits_ {m = 1} ^ M \ log P_J ^ D \ left ({\ Delta r_m \ left | {\ theta _J} \ right.} \ right). $$
(5)
Предполагается, что количество траекторий N будет достаточным для оценки коэффициентов диффузии 34 . Влияние стимуляции цАМФ на коэффициенты диффузии анализировали тем же способом, что и выше, с использованием траекторий, полученных от клеток в указанное время после стимуляции (фиг. 5d).
Анализ диффузии времени жизни одной молекулы
Константы скорости перехода между состояниями и диссоциации мембраны были оценены в соответствии с методом анализа диффузии времени жизни, предложенным ранее 25,35 .Вкратце, используя смещение молекул между t и t + 0,033 с, доля j -го компонента ( j = 1, 2, 3) как функция от t , q D j ( t ), было получено MLE. Коэффициенты диффузии были зафиксированы на значениях, оцененных в диффузионном анализе, описанном выше (таблица 1). Для удобства молекулы, принимающие либо первичное, либо слабосвязанное состояние, рассматривались как переходящие в состояние временного связывания, и q D 2 ( t ) и q D 3 ( t ) для компонентов с умеренным и самым быстрым коэффициентами диффузии соответственно были суммированы и переименованы в q D 2 ' ( t ) (рис.5б). Число молекул, принимающих состояния стабильного или временного связывания, нормированные на N , следует за P 1 ( t ) или P 2 ' ( t ), которые описываются соответственно как
$$ \ begin {array} {l} {\ rm {d}} P_1 \ left (t \ right) / {\ rm {d}} t = - \ left ({k _ {\ mathrm {off1}} + k_ {12 \ prime}} \ right) P_1 \ left (t \ right) + k_ {2 \ prime 1} P_ {2 \ prime} \ left (t \ right), \\ {\ rm {d}} P_ { 2 \ prime} \ left (t \ right) / {\ rm {d}} t = - \ left ({k _ {{\ mathrm {off}} 2 \ prime} + k_ {2 \ prime 1}} \ right ) P_ {2 \ prime} \ left (t \ right) + k_ {12 \ prime} P_1 \ left (t \ right).\ end {array} $$
(6)
k 12 ' и k 2'1 обозначают константу скорости перехода состояния из стабильного в временно связывающее состояние и из переходного в стабильное связывающее состояние, соответственно, и k выкл1 и k off2 ' обозначают константы скорости диссоциации мембраны из стабильного и временного состояний связывания соответственно. Таким образом, общее количество молекул, связанных с клеточной мембраной, нормированное на N , описывается как
$$ \ begin {array} {ccccc} \\ {\ rm {d}} P \ left (t \ right) / {\ rm {d}} t = {\ rm {d}} \ left ({P_1 \ left (t \ right) + P_ {2 \ prime} \ left (t \ right)} \ right) / {\ rm {d}} t \\ \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; = - k _ {\ mathrm {off1}} P_1 \ left (t \ right) - k _ {{\ mathrm {off}} 2 \ prime} P_ {2 \ prime} \ left (t \ right).\\ \ end {array} $$
(7)
q D 1 ( t ), q D 2 ' ( t ) и кривая диссоциации, полученная в ходе анализа срока службы, описанного выше (Рис. 2 ' ( t ) / ( P 1 ( t ) + P 2' ( t )) и P ( t ), которые были получены путем решения одновременное дифференциальное уравнение в MatLab, предполагающее установившееся состояние и с начальными вероятностями при t = 0 из P 1 (0) = a и P 2 ' (0) = 1- a .Данные до t = 2 с использовались для аппроксимации методом наименьших квадратов с трехкратным взвешиванием кривой диссоциации по сравнению с q D 1 ( t ) и q D 2 ' ( t ), поскольку кривая диссоциации демонстрирует экспоненциальный спад (рис. 5b, c).
Статистика
Размеры выборки были определены на основе опыта и соответствующей литературы. Все эксперименты повторяли не менее двух раз с повторением не менее 2 раз.Если не указано иное, критерии включения или исключения данных не использовались. Данные были собраны из случайно выбранных ячеек. Ослепление не производилось. Статистический анализ проводили, как описано выше. Данные представлены в виде средних значений ± SD, SE или средних значений, которые указаны в подписях к рисункам. Статистические сравнения были выполнены с помощью двустороннего критерия Уэлча t , теста отношения правдоподобия или теста регрессионного наклона между группами данных.


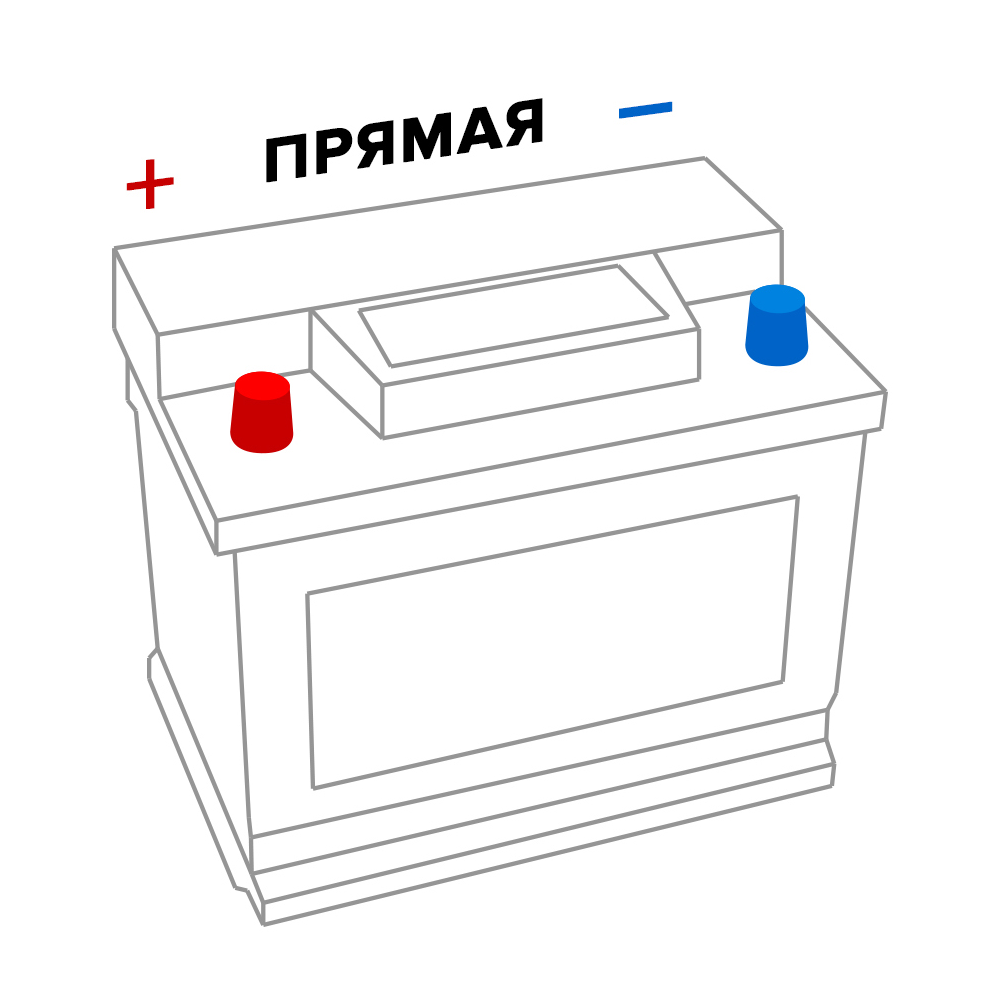 Ее особенность заключается в том, что «плюсовой» вывод установлен слева, а «минусовой» — справа на верхней крышке корпуса АКБ.
Ее особенность заключается в том, что «плюсовой» вывод установлен слева, а «минусовой» — справа на верхней крышке корпуса АКБ.
 Потенциальный барьер — это слой между диодом с PN-переходом, который ограничивает движение электронов через переход.
Потенциальный барьер — это слой между диодом с PN-переходом, который ограничивает движение электронов через переход.